Список индийских изобретений и открытий - List of Indian inventions and discoveries
 |
| История науки и технологии в Индийский субконтинент |
|---|
| По теме |
Этот список индийских изобретений и открытий подробно описывает изобретения, научные открытия и вклад Индии, в том числе древних, классических и постклассических народов на субконтиненте исторически упоминается как Индия и современный индийский штат. Он извлекает из всего культурный и технологическая история Индии, во время которой архитектура, астрономия, картография, металлургия, логика, математика, метрология и минералогия были среди направлений исследований, которыми занимались его ученые.[1] В последнее время наука и технологии в Республике Индия также сосредоточился на автомобильная техника, информационные технологии, коммуникации а также исследования Космос и полярный технологии.
Для целей этого списка изобретения считаются технологическими новинками, разработанными в Индии, и как таковые не включают иностранные технологии, приобретенные Индией посредством контактов. Он также не включает технологии или открытия, разработанные где-либо еще и позже изобретенные отдельно в Индии, а также изобретения индийских эмигрантов в других местах. Изменения в незначительных концепциях дизайна или стиля, а также художественные новшества не отображаются в списках.
Изобретений
Строительство, гражданское строительство и архитектура
- Железный столб Дели: Первым в мире железным столбом был Делиский Железный столб, воздвигнутый во времена Чандрагупта II Викрамадитья (375–413).[2] Столб привлек внимание археологи и материаловеды и был назван «свидетельством мастерства древних индийских кузнецов» из-за его высокой устойчивости к коррозия.[3]
- Stepwell: Самое раннее явное свидетельство происхождения ступенчатого колодца найдено на археологическом участке цивилизации долины Инда в Мохенджодаро в Пакистане[4] и Дхолавира в Индии.[5] Три особенности ступенчатых колодцев на субконтиненте очевидны на одном конкретном месте, заброшенном к 2500 г. до н. Э., Которое объединяет бассейн для купания, ступеньки, ведущие к воде, и фигуры некоторого религиозного значения в одну структуру.[4] В первые века, непосредственно предшествующие нашей эре, буддисты и джайны Индии адаптировали ступенчатые колодцы в своей архитектуре.[4] И колодцы, и форма ритуального купания достигли других частей света с буддизмом.[4] Скальные ступенчатые скважины на субконтиненте датируются периодом от 200 до 400 г. н.э.[6] Впоследствии колодцы в Дханке (550–625 гг. Н. Э.) И ступенчатые пруды на Бхинмал (850–950 гг. Н. Э.).[6]
- Ступа: Происхождение ступы можно проследить до 3-го века до нашей эры в Индии.[7] Он использовался как памятный памятник, связанный с хранением священных реликвий.[7] Архитектура ступы была принята в Юго-восток и Восточная Азия, где он превратился в пагода, буддийский памятник, используемый для сохранения священных реликвий.[7]

- Приземистый туалет: туалеты-площадки над водостоками, в непосредственной близости от колодцев, есть в нескольких домах городов Мохенджодаро и Хараппа с 3-го тысячелетия до нашей эры.[8]
Городская цивилизация Индии восходит к Мохенджодаро и Хараппе, ныне в Пакистане, где 5000 лет назад существовали запланированные городские сообщества. С тех пор древняя индийская архитектура и гражданское строительство продолжали развиваться и расти. Это нашло проявление в строительстве храмов, дворцов и фортов на Индийском полуострове и в соседних регионах. В Древней Индии архитектура и строительство известны как Стхапатья Кала, дословный перевод которого означает искусство строительства (некоторые). Достигнутые в период Кушанской империи и империй Маурьев, индийской архитектуры и строительства в таких регионах, как Белуджистан и Афганистан. Статуи Будды были вырезаны и покрывали целые горные стены и скалы, как Будды Бамиана в Афганистане. смешанные в течение определенного периода времени, построение древнеиндийского искусства и греческих стилей распространилось на Среднюю Азию. С другой стороны, буддизм взял индийский стиль архитектуры и строительства в таких странах, как Шри-Ланка, Индонезия, Малайзия, Вьетнам, Лаос, Камбоджа, Таиланд, Бирма, Китай, Корея и Япония. Ангкор-Ват является живым свидетельством вклада индийского гражданского строительства и архитектуры камбоджийских кхмеров в сферу архитектуры и строительства. На материковой части Индии сегодня есть несколько чудес архитектурного наследия древней Индии, в том числе такие объекты всемирного наследия, как Аджанта, Эллора, Кхаджурахо, Храм Махабодхи, Санчи, Храм Брихадишвары и Махабалипурам
Метрология
- Линейка: Правители сделанные из слоновой кости, использовались цивилизацией долины Инда на территории современной Северо-Западной Индии и Пакистана до 1500 г. до н.э.[9] Раскопки в Лотале (2400 г. до н.э.) обнаружили одну такую линейку с калибровкой примерно на 1/16 дюйма - менее 2 миллиметры.[9] Ян Уайтлоу (2007) считает, что Мохенджодаро линейка разделена на единицы, соответствующие 1,32 дюйма (33,5 мм), и они размечены десятичными делениями с удивительной точностью - с точностью до 0,005 дюйма. Они точно соответствуют шагам «хаста» в 1 3/8 дюйма, традиционно используемым в Южной Индии в древней архитектуре. Древние кирпичи, найденные по всему региону, имеют размеры, соответствующие этим единицам ».[10] Шигео Ивата (2008) далее пишет: «Минимальное деление градуировки, найденное в сегменте линейной меры из слоновой кости, раскопанной в Лотале, составляло 1,79 мм (что соответствует 1/940 сажени), в то время как у фрагмента раковины. -сделанный из Мохенджодаро был 6,72 мм (1/250 сажени), а бронзовый из Хараппы был 9,33 мм (1/180 сажени) ».[11] Гири и меры цивилизации Инда также достигли Персии и Центральная Азия, где они были доработаны.[11]
- Весы: Самые ранние свидетельства существования весов датируются 2400 г. до н.э. – 1800 г. до н.э. в цивилизации долины Инда, до которой банковские операции не выполнялись из-за отсутствия весов.[12]
- Крескограф: Крескограф, устройство для измерения роста растений, было изобретено в начале 20 века бенгальским ученым сэром Джагадиш Чандра Босе.[13][14]
- Часы с благовониями: Часы с благовониями - это устройство для измерения времени, используемое для измерения минут, часов или дней, часы с благовониями обычно использовались в домах и храмах в династические времена. Хотя часы ладана обычно ассоциируются с Китаем, считается, что они возникли в Индии, по крайней мере, в их основной форме, если не в функции.[15][16] Ранние часы с благовониями, найденные в Китае между VI и VIII веками нашей эры - период, когда они появились в Китае, все, кажется, имели Деванагари резьба на них вместо иероглифов китайской печати.[15][16] Само благовоние было завезено в Китай из Индии в первые века нашей эры вместе с распространением буддизма путешествующими монахами.[17][18][19] Эдвард Шафер утверждает, что часы с благовониями, вероятно, были индийским изобретением, переданным в Китай, что объясняет надписи Деванагари на ранних ароматических часах, найденных в Китае.[15] Сильвио Бедини с другой стороны, утверждает, что часы для благовоний были частично получены из печатей для благовоний, упомянутых в Тантрический буддист Священные Писания, которые впервые были обнаружены в Китае после того, как эти священные писания из Индии были переведены на китайский язык, но считает, что функция определения времени печати была включена китайцами.[16]
Металлургия и производство
- Тигельная сталь: Возможно, уже в 300 г. до н. Э. - хотя, безусловно, к 200 г. до н. Э. - высококачественная сталь производилась на юге Индии с помощью того, что европейцы позже назвали тигельной техникой.[20] В этой системе кованое железо высокой чистоты, древесный уголь и стекло смешивались в тигле и нагревались до тех пор, пока железо не расплавилось и не поглотило углерод.[20]

- Wootz Steel: Сталь Wootz - это сверхвысокоуглеродистая сталь и первая форма тигельной стали, производимая с применением и использованием наноматериалы в своей микроструктуре и характеризуется сверхвысоким содержанием углерода, проявляет такие свойства, как сверхпластичность, высокая ударная вязкость и господствует на протяжении тысячелетия на трех континентах - подвиг, который вряд ли превзойдут передовые материалы современной эпохи.[21] Археологические и Тамильский язык литературный данные свидетельствуют о том, что этот производственный процесс уже существовал в Южной Индии задолго до нашей эры, когда Wootz Steel экспортируется из Chera династия и называется Серическое железо в Риме, позже известный как Дамасская сталь в Европе.[22][23][24][25] Исследования репродукции в настоящее время проводятся различными учеными, такими как доктор Олег Шерби и доктор Джефф Уодсворт и Национальная лаборатория Лоуренса Ливермора все провели исследования, пытаясь создать стали с характеристиками, подобными Wootz, но безуспешно JD Verhoeven и Al Pendray достигли определенных успехов в методах реконструкции производства, доказали роль примесей руды в создании модели и воспроизвели сталь Wootz с узоры микроскопически и визуально идентичны одному из древних узоров лезвий.[26]
- Бесшовные небесный шар: Считается одним из самых выдающихся достижений в металлургия, он был изобретен в Индии между 1589 и 1590 годами нашей эры.[27][28] До того, как они были заново открыты в 1980-х годах, современные металлурги считали технически невозможным производить металлические глобусы без каких-либо швы, даже с использованием современных технологий.[28]
- Трубка нарисована технология: индийцы использовали трубчатую технологию для изготовления стеклянных шариков, которая была впервые разработана во 2 веке до нашей эры.[29][30][31]
- Полировка в барабане: Индийцы изобрели метод полировки в 10 веке до нашей эры для массового производства полированных каменных бусин.[32][33][34][35]
- Алмазные сверла: в XII веке до нашей эры или в VII веке до нашей эры индийцы не только усовершенствовали использование алмазных сверл, но и изобрели сверла с двумя алмазными наконечниками для изготовления бусин.[33]
- Алмазная резка и полировка: Технология огранки и полировки алмазов была изобретена в Индии, Ратнапарикша, текст, датированный 6 веком, говорит об огранке алмазов, а Аль-Беруни говорит о методе использования свинцовой пластины для полировки алмазов в 11 веке нашей эры.[36]
Компьютеры и языки программирования
- Дж. Шарп: Визуальный J # (произносится как «джей-острый ") язык программирования был переходным языком для программистов Ява и Visual J ++ языков, чтобы они могли использовать свои существующие знания и приложения на .NET Framework. Он был разработан Хайдарабад -основан Центр разработки Microsoft в Индии в HITEC City в Индии.[37][38]
- Коджо: Коджо это язык программирования и интегрированная среда развития (IDE) для компьютерного программирования и обучения. Коджо является программное обеспечение с открытым исходным кодом. Он был создан и активно развивается Лалит Пант, программистом и учителем, живущим в Дехрадун, Индия.[39][40]
Наука и технология
- Плуг: Самый ранний известный экземпляр вспаханного поля был найден в Калибанган [41]
- Тушь: Известен в Азии с третьего тысячелетия до нашей эры и используется в Индии, по крайней мере, с четвертого века до нашей эры.[42] Маси, ранние чернила в Индии представляли собой смесь нескольких химических компонентов.[42] с углеродной сажей, из которой производятся индийские чернила, получают путем сжигания костей, дегтя, смолы и других веществ.[43][44][45] Документы III века н.э., написанные на Харости, чернилами были раскопаны в Восточный Туркестан, Синьцзян.[46] Практика письма чернилами и острой иглой была распространена в древние времена. Южная Индия.[47] Несколько Джайн сутры в Индии были составлены чернилами.[48]
- СВЧ-связь: Первая публичная демонстрация микроволновой передачи была произведена Джагадиш Чандра Босе в Калькутте в 1895 году, за два года до аналогичной демонстрации Маркони в Англии, и всего через год после Оливер Лодж Памятная лекция по радиосвязи после смерти Герца. Революционная демонстрация Bose формирует основу технологий, используемых в мобильной телефонии, радарах, спутниковой связи, радио, телевещании, Wi-Fi, пультах дистанционного управления и бесчисленном множестве других приложений.[49][50]
- Волоконная оптика: журнал Fortune назвал его одним из семи «невоспетых героев». Д-р Нариндер Сингх Капани, широко известен как «отец волоконной оптики» за его новаторские работы в технологии волоконной оптики.[нужна цитата ]
- Интерферометр сдвига: Изобретено M.V.R.K. Мурти, разновидность бокового Интерферометр сдвига использует лазерный источник для измерения показателя преломления.[51][52]
- Майсорские ракеты: Один из первых металлических цилиндров в железном корпусе. ракеты были развернуты Типу Султан армия, правитель Южной Индии Королевство Майсур, и его отца Хайдер Али, в 1780-х гг. Он успешно использовал эти ракеты в железном корпусе против более крупных сил Британская Ост-Индская компания вовремя Англо-майсурские войны. Майсурские ракеты того периода были намного более совершенными, чем то, что видели британцы, главным образом из-за использования железных трубок для удерживания топлива; это позволило увеличить тягу и дальность полета ракеты (до 2 км). После окончательного поражения Типу в Четвертая англо-майсурская война и захват железных ракет Майсура, они оказали влияние на британские ракетные разработки, вдохновив Ракета Конгрева, и вскоре были введены в Наполеоновские войны.[53]

- Шампунь: Слово шампунь на английском языке происходит от Хиндустани чампо (चाँपो [tʃãpoː]),[54] и датируется 1762 годом.[55] Различные травы и их экстракты использовались в качестве шампуней с древних времен в Индии. Очень эффективный ранний шампунь получали кипячением. Сапиндус с сушеными индийский крыжовник (амла) и несколько других трав, используя процеженный экстракт. Сапиндус, также известный как мыльница или мыльный орех, называется Ксуна (Санскрит: क्षुण)[56] в древнеиндийских текстах и его фруктовая мякоть содержат сапонины, натуральные поверхностно-активные вещества. Экстракт Ксуны создает пену, которую в индийских текстах называют фенака (Санскрит: फेनक),[57] делает волосы мягкими, блестящими и послушными. Другими продуктами, используемыми для очищения волос, были шикакаи (Акация кончинная ), мыльные орехи (Сапиндус ), гибискус цветы,[58][59] рита (Сапиндус мукоросси ) и араппу (Albizzia amara).[60] Гуру Нанак, пророк-основатель и первый Гуру из Сикхизм, ссылался на мыльное дерево и мыло в 16 веке.[61] Мытье волос и массаж тела (чампу) во время ежедневного мытья стриптизом были потаканием ранним колониальным торговцам в Индии. Когда они вернулись в Европу, они представили свои недавно усвоенные привычки, включая уход за волосами, который они назвали шампунем.[62]
- Стремя пальца ноги: Самое раннее известное проявление стремени, представлявшего собой петлю на большом пальце ноги, использовалось в Индии еще в 500 г. до н. Э.[63] или, возможно, к 200 г. до н.э., согласно другим источникам.[64][65] Это древнее стремя состояло из веревки с петлей для большого пальца ноги, которая находилась у основания седла из волокна или кожи.[65] Такая конфигурация сделала его подходящим для теплого климата большей части Индии, где люди ездили босиком на лошадях.[65] Пара мегалитических железных прутьев, изогнутых в два раза, с кривизной на каждом конце, раскопанных в Джунапани в центральном индийском штате Мадхья-Прадеш считались стременами, хотя могли быть и чем-то другим.[66] Буддийская резьба в храмах Санчи, Матхура и Пещеры Бхаджа датируется периодом между I и II веками до нашей эры. Фигурки всадников верхом в замысловатых седлах и ногах, проскальзывающих под подпругами.[67][68][69] Сэр Джон Маршалл описал рельеф Санчи как «самый ранний пример примерно за пять веков использования стремена в любой части мира».[69] В I веке н.э. у всадников в северной Индии, где зимы иногда бывают долгими и холодными, зафиксировано, что их ноги в ботинках прикреплялись к стременам с крючками.[64] Однако форма, концепция примитивного индийского стремени распространилась на запад и восток, постепенно превращаясь в современное стремени.[65][68]
Генетика
- Pseudomonas putida: Индийский (бенгальский) изобретатель и микробиолог. Ананда Мохан Чакрабарти создал вид искусственных микроорганизмов для расщепления сырой нефти.[70] Он генно-инженерный[71][72][73][74][75][76] новый вид Псевдомонады бактерии (" масло - поедающие бактерии ») в 1971 году.[77] Верховный суд США выдал патент на изобретение Чакрабарти, хотя это был живой вид. Суд постановил, что открытие Чакрабарти было «не делом рук природы, а его собственным ...». Изобретатель Чакрабарти получил свой патент в 1980 году.[78](видеть Даймонд против Чакрабарти )
Игры
- Чатуранга: Предшественник шахматы возникла в Индии во время Династия Гуптов (ок. 280–550 гг. н. э.).[79][80][81][82] Оба персы и Арабов приписывают происхождение игры в шахматы индейцам.[81][83][84] Слова для «шахмат» в Древнеперсидский и арабский находятся болтовня и Шатрандж соответственно - термины, полученные из Caturaga в санскрит,[85][86] что буквально означает армия из четырех дивизий или же четыре корпуса.[87][88] Шахматы распространились по всему миру, и вскоре начали складываться многие варианты игры.[89] Эта игра была представлена Ближний Восток из Индии и стал частью княжеского или придворного образования Персидский благородство.[87] Буддист паломники Шелковый путь торговцы и другие несли его Дальний Восток где он был преобразован и ассимилирован в игру, в которую часто играли на пересечении линий доски, а не внутри квадратов.[89] Чатуранга попала в Европу через Персию, Византийская империя и расширение Арабский империя.[88][90] Мусульмане перенес Шатрандж в Северная Африка, Сицилия и Испания к 10 веку, где она приняла свою последнюю современную форму шахмат.[89]
- Кабадди: Игра Кабадди возникла в Индии в доисторические времена.[91] Предложения о том, как она превратилась в современную форму, варьируются от упражнений по борьбе, военных учений и коллективной самообороны, но большинство авторитетов согласны с тем, что игра существовала в той или иной форме в Индии в период между 1500 и 400 годами до нашей эры.[91]
- Людо: Пачиси возникла в Индии в VI веке.[92] Самым ранним свидетельством этой игры в Индии является изображение досок в пещерах Аджанты.[92] Вариант этой игры под названием Ludo появился в Англии во времена британского владычества.[92]
- Змеи и лестницы: Вайкунта пали Змеи и лестницы возникли в Индии как игра, основанная на морали.[93] Во время британского правления в Индии эта игра попала в Англию и в конечном итоге была представлена в Соединенных Штатах Америки пионером игры. Милтон Брэдли в 1943 г.[93]
- Костюмы игра: Кридапатрам - ранний костюмы игра, сделанная из расписных тряпок, изобретена еще в Древней Индии. Период, термин Кридапатрам буквально означает «разрисованные тряпки для игр».[94][95][96][97][98] Бумажные игральные карты впервые появились в Восточной Азии в IX веке.[94][99] Средневековая индийская игра Ганджифа, или игральные карты, впервые упоминается в 16 веке.[100]
Производство ткани и материалов
- Кнопка: Декоративные пуговицы - из морская ракушка - использовались в Цивилизация долины Инда в декоративных целях к 2000 г. до н.э.[101] На некоторых пуговицах были вырезаны геометрические формы и в них были проделаны отверстия, чтобы их можно было прикрепить к одежде с помощью нитки.[101] Ян Макнил (1990) считает, что: «Пуговица изначально использовалась скорее как украшение, чем как застежка, самая ранняя из известных находок была найдена в Мохенджо-Даро в Долина Инда. Он сделан из изогнутой раковины и ему около 5000 лет ".[102]

- Калико: Калико возник на субконтиненте в 11 веке и упоминается в индийской литературе писателем 12 века Хемачандрой. Он упомянул принты на ситцевой ткани, выполненные в стиле лотоса.[103] Индийские торговцы текстилем торговали ситцевыми тканями с африканцами к 15 веку, а ситцевые ткани от Гуджарат появился в Египет.[103] Торговля с Европой началась с 17 века.[103] В Индии ситцевая ткань возникла в Кожикоде.[103]
- Кардочесальные устройства: Историк науки Джозеф Нидхэм приписывает изобретение смычковых инструментов, используемых в текстильной технологии, Индии.[104] Самые ранние свидетельства использования луковых инструментов для чесания относятся к Индии (II век н.э.).[104] Эти кардочесальные устройства, называемые Каман и дхунаки ослабит текстуру волокна с помощью вибрирующей струны.[104]
- Чарха (Вращающееся колесо): изобретено в Индии между 500 и 1000 годами нашей эры.[105]
- Ситец: Ситец происходит из набивной хлопчатобумажной ткани ситца в Индии.[106] Происхождение слова ситец сам из Язык хинди слово चित्र् (читр), что означает изображение.[106][107]
- Муслин: Ткань была названа в честь города, в котором европейцы впервые с ней столкнулись, Мосул, в том, что сейчас Ирак, но на самом деле ткань произошла из Дакка в том, что сейчас Бангладеш.[108][109] В 9 веке Арабский купец по имени Сулейман отмечает происхождение материала в Бенгалия (известный как Румл в арабский ).[109]

- Палампор: पालमपोर् (язык хинди) индийского происхождения[110] был импортирован в западный мир - известную Англию и Колониальная Америка -из Индии.[111][112] В Англии 17-го века эти расписанные вручную хлопковые ткани повлияли на дизайн работы местных жителей.[111] Судоходные суда из Индии также доставляли палампор в колониальную Америку, где он использовался в квилтинг.[112]
- Молитвенные флаги: The Буддист сутры, написанные на ткани в Индии, были переданы в другие регионы мира.[113] Эти сутры, написанные на знаменах, явились источником молитвенных флагов.[113] Легенда приписывает происхождение молитвенного флага Будда Шакьямуни, чьи молитвы были написаны на боевых флагах, используемых дэвы против своих противников, асуры.[114] Легенда, возможно, дала индейцу бхикку причина нести «небесное» знамя как способ показать свою приверженность ахимса.[115] Это знание было перенесено в Тибет к 800 г. н.э., а фактические флаги были введены не позднее 1040 г. н.э., где они были дополнительно изменены.[115] Индийский монах Атиша (980–1054 гг.) Ввел в Тибет индийскую практику печати на тканевых молитвенных флагах.[114]
- Одноместный хлопковый джин: The Пещеры Аджанты Индии есть свидетельства того, что к V веку использовался только один роликовый хлопкоочиститель.[116] Этот хлопкоочиститель использовался в Индии до тех пор, пока не появились новинки в виде джинов с ножным приводом.[117] Хлопковый джин был изобретен в Индии как механическое устройство, известное как чархи, точнее говоря, "деревянно-червячный ролик". В некоторых частях Индии это механическое устройство приводилось в движение силой воды.[104]
Благополучие
- Индийские клубы: Индийская дубинка, которая появилась в Европе в 18 веке, использовалась коренными индийскими солдатами задолго до ее появления в Европе.[118] Вовремя Британский Радж Британские офицеры в Индии выполняли гимнастические упражнения с дубинками для поддержания физической формы.[118] Из Британии использование клюшек распространилось на весь остальной мир.[118]
- Йога: Йога как физическая, умственная и духовная практика зародилась в древняя Индия.[119]
- Медитация: Древнейшими документально подтвержденными свидетельствами практики медитации являются настенные рисунки в Индийский субконтинент приблизительно от 5000 до 3500 г. до н.э., изображающие людей, сидящих в медитативных позах с полузакрытыми глазами.[120]
Открытия
- Кашемир: Кашемировое волокно, также известное как пашм или же пашмина для использования в шалях ручной работы в Кашмире, Индия.[121] Шерстяные шали из шерсти в Индии Кашмир найти письменные упоминания между III веком до нашей эры и XI веком нашей эры.[122] Тем не менее, основателем индустрии кашемировой шерсти традиционно считается правитель Кашмира 15 века. Зайн-уль-Абидин, нанявших ткачей из Центральная Азия.[122]
- Выращивание хлопка: Хлопок выращивали жители Цивилизация долины Инда посредством V тысячелетие до н. Э. – 4 тысячелетие до н. Э..[123] Индийская хлопковая промышленность была хорошо развита, и некоторые методы, используемые при прядении и производстве хлопка, продолжали практиковаться до современной индустриализации Индии.[124] Задолго до Наша эра, использование хлопчатобумажных тканей распространилось из Индии в Средиземноморье и дальше.[125]
- Краситель индиго: Индиго, синий пигмент и краситель, использовался в Индии, которая также была одним из первых крупных центров его производства и обработки.[126] В Индигофера красильная сорт Индиго был одомашнен в Индии.[126] Индиго, используемый как краситель, попал в Греки и Римляне через различные торговые пути и ценился как предмет роскоши.[126]
- Выращивание джута: Джут выращивали в Индии с древних времен.[127] Сырой джут экспортировался в западный мир, где он использовался для изготовления веревки и снасти.[127] Индийская джутовая промышленность, в свою очередь, была модернизирована во время британского правления в Индии.[127] Регион Бенгалия был основным центром выращивания джута и оставался им до модернизации джутовой промышленности Индии в 1855 году, когда Калькутта стал центром обработки джута в Индии.[127]
- Сахарная очистка: Сахарный тростник родом из тропических Южная Азия и Юго-Восточная Азия,[128] с разными видами, происходящими из Индии, и S. edule и S. officinarum из Новая Гвинея.[128] Процесс производства кристаллизованного сахара из сахарного тростника был открыт ко времени Императорские Гупты,[129] и самое раннее упоминание засахаренного сахара происходит из Индии.[130] Вскоре процесс был перенесен в Китай с путешествующими буддийскими монахами.[130] Китайские документы подтверждают как минимум две миссии в Индию, начатые в 647 году н.э., для получения технологии для рафинирования сахара.[131] Каждая миссия возвращалась с результатами по переработке сахара.[131]
Математика
| Система счисления | Числа | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Тамильский | ೦ | ௧ | ௨ | ௩ | ௪ | ௫ | ௬ | ௭ | ௮ | ௯ |
| Гурмукхи | о | ੧ | ੨ | ੩ | ੪ | ੫ | ੬ | ੭ | ੮ | ੯ |
| Ория (Одиа) | ୦ | ୧ | ୨ | ୩ | ୪ | ୫ | ୬ | ୭ | ୮ | ୯ |
| Бенгальский | ০ | ১ | ২ | ৩ | ৪ | ৫ | ৬ | ৭ | ৮ | ৯ |
| Ассамский | ০ | ১ | ২ | ৩ | ৪ | ৫ | ৬ | ৭ | ৮ | ৯ |
| Деванагари | ० | १ | २ | ३ | ४ | ५ | ६ | ७ | ८ | ९ |
| Гуджарати | ૦ | ૧ | ૨ | ૩ | ૪ | ૫ | ૬ | ૭ | ૮ | ૯ |
| тибетский | ༠ | ༡ | ༢ | ༣ | ༤ | ༥ | ༦ | ༧ | ༨ | ༩ |
| Брахми | ||||||||||
| телугу | ౦ | ౧ | ౨ | ౩ | ౪ | ౫ | ౬ | ౭ | ౮ | ౯ |
| Каннада | ೦ | ೧ | ೨ | ೩ | ೪ | ೫ | ೬ | ೭ | ೮ | ೯ |
| Малаялам | ൦ | ൧ | ൨ | ൩ | ൪ | ൫ | ൬ | ൭ | ൮ | ൯ |
| Бирманский | ၀ | ၁ | ၂ | ၃ | ၄ | ၅ | ၆ | ၇ | ၈ | ၉ |
| Кхмерский | ០ | ១ | ២ | ៣ | ៤ | ៥ | ៦ | ៧ | ៨ | ៩ |
| Тайский | ๐ | ๑ | ๒ | ๓ | ๔ | ๕ | ๖ | ๗ | ๘ | ๙ |
| Лаосский | ໐ | ໑ | ໒ | ໓ | ໔ | ໕ | ໖ | ໗ | ໘ | ໙ |
| Балийский | ᭐ | ᭑ | ᭒ | ᭓ | ᭔ | ᭕ | ᭖ | ᭗ | ᭘ | ᭙ |
| Сантали | ᱐ | ᱑ | ᱒ | ᱓ | ᱔ | ᱕ | ᱖ | ᱗ | ᱘ | ᱙ |
| Яванский | ꧐ | ꧑ | ꧒ | ꧓ | ꧔ | ꧕ | ꧖ | ꧗ | ꧘ | ꧙ |


- Нуль, символ: индейцы первыми использовали ноль как символ и в арифметических операциях,[нужна цитата ] хотя вавилоняне использовали ноль для обозначения «отсутствующего».[132] Раньше для обозначения нуля использовался пробел, позже, поскольку пробел создавал путаницу в более сложных документах, для обозначения нуля использовалась точка, которая сначала использовалась в Бахшалинская рукопись.[133] Использование нуля в манускрипте Бахшали датируется между 3 и 4 веками, что делает его самым ранним известным использованием символа.[134]
- Квадратные уравнения: индийский математик Шридхарачарья вывел квадратную формулу, используемую для решения квадратных уравнений.[135][136]
- Тест на простоту AKS: Тест на простоту AKS - это детерминированный доказывающий примитивность алгоритм созданы и опубликованы тремя Индийский технологический институт Канпур компьютерные ученые, Маниндра Агравал, Нирадж Каял, и Нитин Саксена 6 августа 2002 г. в газете под названием PRIMES находится в P.[137][138] Комментируя влияние этого открытия, Пол Лейланд отметил: «Одна из причин ажиотажа в математическом сообществе заключается не только в том, что этот алгоритм решает давнюю проблему, но и делает это гениально просто. Теперь все задаются вопросом, что еще было упущено из виду».[138][139]
- Конечная разница Интерполяция: Индийский математик Брахмагупта представил то, что возможно является первым экземпляром[140][141] конечно-разностной интерполяции около 665 г. н.э.[142]
- Алгебраические сокращения: Математик Брахмагупта начал использовать аббревиатуры для неизвестных к 7 веку.[143] Он использовал сокращения для множества неизвестных, встречающихся в одной сложной задаче.[143] Брахмагупта также использовал аббревиатуры для квадратные корни и кубические корни.[143]
- Константа Сешадри: В алгебраическая геометрия, константа Сешадри является инвариантом обильного линейного расслоения L в точке P на алгебраическое многообразие Название дано в честь индийского математика. К. С. Сешадри.
- Теорема Басу: Теорема Басу, результат Дебабрата Басу (1955) заявляет, что любая полная достаточная статистика не зависит от какой-либо дополнительной статистики.[144][145]
- Теорема Ролля: Бхаскара II приписывают знание Теорема Ролля хотя он назван в честь Мишель Ролль который описал с недостаточными доказательствами и позже был доказан Коши.[146]
- Теорема Косамби-Карунена-Лоэва: также известная как Теорема Карунена – Лоэва. Теорема Косамби-Карунена-Лоэва представляет собой представление случайного процесса в виде бесконечной линейной комбинации ортогональные функции, аналогично Ряд Фурье представление функции на ограниченном интервале. Стохастические процессы, заданные бесконечными рядами такой формы, были первыми.[147] рассматривается Дамодар Дхармананда Косамби.[148]
- Тождество Брахмагупты – Фибоначчи, Формула Брахмагупты, Матрица брахмагупты, и Теорема Брахмагупты: Обнаружен индийским математиком Брахмагуптой (598–668 гг. Н. Э.).[149][150][151][152]
- Метод чакравалы: Метод Чакравалы, циклический алгоритм решения неопределенный квадратные уравнения обычно приписывается Бхаскара II, (ок. 1114 - 1185 г. н.э.)[153][154][155] хотя некоторые приписывают это Джаядева (ок. 950 ~ 1000 г. н. э.).[156] Джаядева указал, что подход Брахмагупты к решению уравнений этого типа даст бесконечно большое количество решений, для которых он затем описал общий метод решения таких уравнений.[157] Позже метод Джаядевы был усовершенствован Бхаскарой II в его Биджаганита трактат, известный как метод Чакравалы, чакра (происходит от чакрах चक्रं) означает колесо в санскрит, относящиеся к цикличности алгоритма.[157][158] Ссылаясь на метод Чакравалы, Э. О. Селенуис утверждал, что ни одно европейское выступление во времена Бхаскары или намного позже не достигло его удивительной высоты математической сложности.[153][157][159]
- Теорема Пифагора - теорема Пифагора, которую, как полагают, дал математик, известный как Пифитагор, на самом деле неверна. Она была давным-давно изложена в своей книге мудрецом Баудхаяной.
- Магическое открытие индийской математики: числа 495 и 6174. Индийский математик Даттарая Рамчандра Капрекар обнаружил, что число 6174 достигается после многократного вычитания наименьшего числа из наибольшего числа, которое может быть образовано из любых четырех цифр, которые не все одинаковы. Число 495 аналогично достигается для трехзначного числа.
- Индуистская система счисления: С десятичный место и символ нуля, эта система была предком широко используемых Арабская цифра система. Он был разработан на Индийском субконтиненте между 1 и 6 веками нашей эры.[160][161]
- Десятичный знак: Практика использования десятичного знака происходит от десятичная система используется в Индийская математика.[162]
- Числа Фибоначчи: Эта последовательность была впервые описана Вираханка (ок. 700 г. н. э.), Гопала (ок. 1135), и Хемачандра (ок. 1150 г.),[163] как результат более ранних работ по санскритской просодии Пингала (ок. 200 г. до н. э.).
- Закон знаков в умножении: самое раннее использование обозначения для отрицательных чисел, как вычитаемое, приписывается учеными китайцам, начиная со 2 века до нашей эры.[164] Подобно китайцам, индийцы использовали отрицательные числа для вычитания, но были первыми, кто установил «закон знаков» в отношении умножения положительных и отрицательных чисел, который не появлялся в китайских текстах до 1299 года.[164] Индийские математики знали об отрицательных числах к 7 веку,[164] и их роль в математических проблемах долга была понята.[165] Сформулированы наиболее последовательные и правильные правила работы с отрицательными числами,[166] Распространение этих правил побудило арабских посредников передать его Европе.[165] например (+) × (-) = (-), (-) × (-) = (+) и т. д.
- Серия Мадхава: Бесконечный ряд для π и тригонометрического синус, косинус, и арктангенс теперь приписывается Мадхаве из Сангамаграмы (ок. 1340–1425) и его школе астрономии и математики в Керале.[167][168] Он использовал расширение серии чтобы получить выражение для π в виде бесконечного ряда.[167] Их рациональное приближение к ошибка для конечной суммы их рядов представляют особый интерес. Они манипулировали термином ошибки, чтобы получить более быстрый сходящийся ряд для π.[169] Они использовали улучшенный ряд, чтобы получить рациональное выражение,[169] для π исправить до одиннадцати знаков после запятой, т.е. .[170][171] Мадхава Сангамаграмы и его преемники в Керальская школа астрономии и математики использовали геометрические методы для получения приближений большой суммы для синуса, косинуса и арктангенса. Они обнаружили ряд частных случаев рядов, позже выведенных из рядов Брука Тейлора. Они также нашли приближение Тейлора второго порядка для этих функций и приближение Тейлора третьего порядка для синуса.[172][173][174]
- Треугольник Паскаля: Описан в VI веке н.э. Варахамихира[175] а в 10 веке Халаюда,[176] комментируя неясную ссылку Пингала (автор более ранней работы по просодии) к «Меру-прастара», или «Лестнице на гору Меру», по отношению к биномиальным коэффициентам. (Он был также независимо обнаружен в 10 или 11 веке в Персии и Китае.)
- Уравнение Пелла, интегральное решение для: Около тысячи лет назад Пеллс время, индийский ученый Брахмагупта (598–668 н. э.) смог найти интегральные решения Vargaprakṛiti (Уравнение Пелла):[177][178] куда N неквадратное целое число, в его Брахма-спхуса-сиддханта научный труд.[178]
- Рамануджан тета-функция, Рамануджан премьер, Рамануджан суммирование, График Рамануджана и Сумма Рамануджана: Открыто индийским математиком. Шриниваса Рамануджан в начале 20 века.[179]
- Граф Шриханде: График изобретен индийским математиком С.С.Шриханде в 1959 году.
- Подписать соглашение: Символы, знаки и математические обозначения использовались в ранней форме в Индии к 6 веку, когда математик-астроном Арьябхата рекомендовал использовать буквы для обозначения неизвестных величин.[143] К 7 веку Брахмагупта уже начал использовать аббревиатуры для неизвестных, даже для нескольких неизвестных, возникающих в одной сложной проблеме.[143] Брахмагупте также удалось использовать сокращения для квадратных корней и кубических корней.[143] К VII веку дроби были написаны аналогично современным временам, за исключением полосы, разделяющей числитель и знаменатель.[143] Символ точки для отрицательные числа также был нанят.[143] В Бахшалинская рукопись отображает крест, очень похожий на современный знак «+», за исключением того, что он символизирует вычитание, когда пишется сразу после затронутого числа.[143] Знак «=» для равенства не существует.[143] Индийская математика была передана в исламский мир, где изначально эти обозначения редко принимались, а писцы продолжали писать математику полностью и без символов.[180]
- Современное элементарная арифметика: Modum indorum, или метод индусов для арифметических операций, был популяризирован Аль-Хорезми и Аль-Кинди посредством их соответствующих работ, таких как Аль-Хорезми «О вычислении с помощью индусских цифр» (ок. 825 г.), «Об использовании индийские цифры (ок. 830)[181] еще в VIII и IX веках. Они, среди прочих работ, способствовали распространению индийской системы арифметики на Ближнем Востоке и на Западе. Значение развития позиционной системы счисления описано французским математиком. Пьер Симон Лаплас (1749–1827), который писал:
"Это Индия дала нам наивный метод выражения всех чисел с помощью десяти символов, при этом каждому символу присваивается значение положения, а также абсолютное значение; глубокая и важная идея, которая кажется нам такой простой сейчас, когда мы игнорировать его истинные достоинства, но сама его простота, большая легкость, которую он придавал всем вычислениям, ставит нашу арифметику на первое место среди полезных изобретений, и мы оценим величие этого достижения, когда вспомним, что оно ускользнуло от гения Архимед и Аполлоний, двое величайших умов древности ».
- Тригонометрические функции : The тригонометрический функции синус и Версина возник в Индийская астрономия, адаптированный из полноаккордных греческих версий (к современным полуккордовым версиям). Их подробно описал Арьябхата в конце 5 века, но, вероятно, были разработаны ранее в Сиддханты, астрономические трактаты 3-го или 4-го века.[182][183] Позже астроном VI века Варахамихира открыл несколько основных тригонометрических формул и тождеств, таких как sin ^ 2 (x) + cos ^ 2 (x) = 1.[175]
- Формальные системы: Панини приписывают создание первого Формальная система в мире.
Лекарство
- Аюрведический и Сиддха медицина: Аюрведа и Сиддха - древние системы медицины, практикующиеся в Южной Азии. Аюрведические идеи можно найти в индуистских текстах.[184] (середина первого тысячелетия до нашей эры). Аюрведа развивалась на протяжении тысяч лет и до сих пор практикуется. В интернационализированной форме его можно рассматривать как дополнительная и альтернативная медицина. В деревнях, вдали от городских центров, это просто «лекарство». Санскритское слово आयुर्वेदः (аюр-ведах) означает "знание (веда) на долголетие (Аюр)".[185] Сиддха в основном распространена в Южной Индии и передается в текстах на тамильском, а не на санскрите. Травы и минералы являются основным сырьем для терапевтической системы сиддхов, происхождение которой может быть датировано ранними веками нашей эры.[186][187]
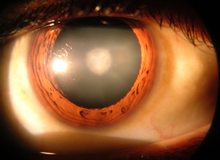
- Операция по удалению катаракты: Хирургия катаракты была известна индийскому врачу Сушруте (6 век до н.э.).[188] В Индии операцию по удалению катаракты выполняли с помощью специального инструмента, называемого Джабамукхи Салака, изогнутая игла, используемая для ослабления линзы и выталкивания катаракты из поля зрения.[189] Позже глаз пропитывали теплым маслом и перевязывали.[189] Хотя этот метод оказался успешным, Сусрута предупредил, что операцию по удалению катаракты следует проводить только в случае крайней необходимости.[189] Греческие философы и ученые отправились в Индию, где эти операции были выполнены врачами.[189] Удаление катаракты хирургическим путем также было введено в Китай из Индии.[190]
- Древняя стоматология: The Цивилизация долины Инда (IVC) предоставил доказательства того, что стоматология практиковалась еще в 7000 году до нашей эры. Сайт IVC в Mehrgarh указывает на то, что эта форма стоматологии включала лечение заболеваний, связанных с зубами, с помощью луковые сверла управляемый, возможно, опытными мастерами по бисероплетению.
- Лекарство от Проказа: Kearns & Nash (2008) утверждают, что первое упоминание о проказе описано в индийском медицинском трактате. Сушрута Самхита (6 век до н.э.).[191] Тем не мение, Oxford Illustrated Companion to Medicine считает, что упоминание о проказе, а также о ритуальных средствах от нее были описаны в Атхарва-веда (1500–1200 гг. До н.э.), написанные до Сушрута Самхита.[192]
- Пластическая хирургия: Процедуры пластической хирургии сломанного носа впервые упоминаются в Эдвин Смит Папирус,[193] транскрипция древнеегипетского медицинского текста, одного из старейших известных хирургических трактатов, датированного Старое королевство от 3000 до 2500 г. до н.э.[194] Пластические операции проводились в Индии к 2000 году до нашей эры.[195] Система наказания путем деформации тела злоумышленника могла привести к увеличению спроса на эту практику.[195] Хирург Сушрута внес вклад в основном в области пластической хирургии и хирургии катаракты.[196] Медицинские работы Сушруты и Чарака были переведены на арабский язык во время Аббасидский халифат (750 г. н.э.).[197] Эти переведенные на арабский язык произведения попали в Европу через посредников.[197] В Италия семья Бранка Сицилия и Гаспаре Тальякоцци из Болоньи познакомились с техниками Сушруты.[197]
- Лечение литиаза: Самая ранняя операция по лечению литиаза или образования камней в теле также проводится в Сушрута Самхита (6 век до н.э.).[198] Операция заключалась в обнажении и прохождении дна мочевого пузыря.[198]
- Висцеральный лейшманиоз, лечение: Индийский (бенгальский) практикующий врач. Упендранатх Брахмачари (19 декабря 1873 г. - 6 февраля 1946 г.) был номинирован на Нобелевская премия по физиологии и медицине в 1929 г. за открытие уреастибамина (сурьма сложный для лечения кала азар ) и новое заболевание, посткалаазарский кожный лейшманоид ».[199] Лекарством Брахмачари от висцерального лейшманиоза была соль мочевины пара-амино-фенилстибновой кислоты, которую он назвал мочевиной стибамином.[200] После открытия мочевины стибамина висцеральный лейшманиоз был в значительной степени искоренен в мире, за исключением некоторых слаборазвитых регионов.[200]
- Стенокардия: Состояние было названо «хритсула» в древней Индии и описано Сушрута (6 век до н.э.).[196]
Добыча полезных ископаемых
- Добыча алмазов и алмазные инструменты: алмазы были впервые обнаружены и добыты в центральной Индии,[201][202][203] где значительные россыпи камня могли быть найдены вдоль рек Penner, Кришна и Годавари. Неизвестно, когда алмазы были впервые добыты в Индии, хотя, по оценкам, это было не менее 5000 лет назад.[204] Индия оставалась единственным источником алмазов в мире до открытия алмазов в Бразилии в 18 веке.[205][206][207] Голконда служил важным центром алмазов в Центральная Индия.[208] Затем алмазы экспортировались в другие части мира, включая Европу.[208] Первые упоминания об алмазах в Индии происходят из санскрит тексты.[209] В Арташастра из Каутиля упоминает торговлю алмазами в Индии.[207] Буддист в произведениях, датируемых IV веком до нашей эры, он упоминается как широко известный и драгоценный камень, но не упоминаются детали огранки алмазов.[201] Другое индийское описание, написанное в начале 3-го века, описывает прочность, регулярность, блеск, способность царапать металлы и хорошие преломляющие свойства как желательные качества алмаза.[201] В китайском произведении III века до нашей эры упоминается: «Иностранцы носят его [алмаз], веря, что он может отразить дурное влияние».[201] Китайцы, которые не нашли алмазов в своей стране, изначально использовали алмазы как «нож для резки нефрита», а не как драгоценный камень.[201]
- Добыча цинка и лечебный цинк: Цинк впервые был выплавлен из цинковой руды в Индии.[210] Цинковые рудники Завара, около Удайпур, Раджастхан, были активны в раннехристианскую эпоху.[211][212] Есть ссылки на использование цинка в медицинских целях в Чарака Самхита (300 г. до н.э.).[213] В Расаратна Самучкая который восходит к тантрическому периоду (c. 5-13 века н.э.) объясняет существование двух типов руд металлического цинка, одна из которых идеальна для добычи металла, а другая используется в лечебных целях.[213][214] Индия должна была расплавить первый цинк, полученный в результате длительного опыта древней алхимии, с помощью процесса дистилляции, передовой техники. Древние персы также пытались восстановить оксид цинка в открытой печи, но безуспешно. Завар в долине Тири в Раджастане - первое известное старое предприятие по выплавке цинка в мире. Дистилляционная техника производства цинка восходит к XII веку нашей эры и является важным вкладом Индии в мир науки.
Наук
- Сила тяжести: Арьябхата впервые определили силу, чтобы объяснить, почему объекты не вращаются при вращении Земли, Брахмагупта описал гравитацию как силу притяжения и использовал термин гурутвакарнах для гравитации.[215][216][217] Арьябхата был первым, кто разработал гелиоцентрический модель солнечной системы, в которой планеты вращаются вокруг своих осей и следуют по орбитам вокруг Солнца, в то время как Луна вращается вокруг Земли в эпициклы.
- Нитрит аммония, синтез в чистом виде: Прафулла Чандра Рой синтезированный NH4НЕТ2 в чистом виде и стал первым ученым, сделавшим это.[218] До синтеза нитрита аммония Рэем считалось, что это соединение подвергается быстрому термическому разложению с выделением азота и воды.[218]
- Переменные Аштекара: В теоретической физике Аштекарские (новые) переменные, названные в честь Абхай Аштекар кто их изобрел, представляют собой необычный способ переписать метрику на трехмерных пространственных срезах в терминах SU (2) калибровочное поле и его дополнительная переменная. Переменные Аштекара являются ключевым строительным блоком петля квантовой гравитации.
- Атом: Один из замечательных ученых древней Индии был Канаде, который, как говорят, разработал атомную теорию за несколько столетий до рождения Джона Далтона. Он предположил существование Ану или небольших неразрушимых частиц, похожих на атом. Он также объяснил, что у Ану может быть два состояния - абсолютный покой и состояние движения. Он писал, что атомы одного и того же вещества соединяются друг с другом особым образом, образуя синхронизированные двянука (двухатомные молекулы), которые затем генерируют трянука (трехатомные молекулы).[нужна цитата ]
- Баланс магнитных помех Бхатнагар-Матур: совместно изобретен Шанти Сваруп Бхатнагар и К. В 1928 году в Матхуре, так называемые «магнитные весы Бхатнагара-Матура», были современным прибором, используемым для измерения различных магнитных свойств.[219] Первое появление этого инструмента в Европе произошло на Королевское общество выставка в Лондоне, где позже продавалась британская фирма Messers Adam Hilger and Co, Лондон.[219]
- Бхабха рассеяние: В 1935 году индийский физик-ядерщик. Хоми Дж. Бхабха опубликовал статью в Труды Королевского общества, серия А, в котором он провел первый расчет для определения сечения электрон-позитронного рассеяния.[220] Электрон-позитронное рассеяние позже было названо рассеянием Бхабхи в честь его вклада в эту область.[220]
- Статистика Бозе – Эйнштейна, конденсат: 4 июня 1924 г. индийский физик Сатьендра Нат Бос отправил короткую рукопись по адресу Альберт Эйнштейн озаглавленный Закон Планка и световая квантовая гипотеза ищет влияние Эйнштейна, чтобы опубликовать его после того, как он был отклонен престижным журналом Философский журнал.[221] В документе представлено то, что сегодня называется Статистика Bose, который показал, как его можно использовать для получения спектра черного тела Планка, исходя из предположения, что свет состоит из фотоны.[221][222] Эйнштейн, признав важность статьи, сам перевел ее на немецкий и представил от имени Бозе в престижную Zeitschrift für Physik.[221][222] Позднее Эйнштейн применил принципы Бозе к частицам с массой и быстро предсказал Конденсат Бозе-Эйнштейна.[222][223]
- Бозон: Название бозон было придумано Поль Дирак[224] отметить вклад Индийский физик Сатьендра Нат Бос.[225][226] В квантовая механика, а бозон (/ˈбoʊsɒп/,[227] /ˈбoʊzɒп/[228]) - частица, которая следует за Статистика Бозе – Эйнштейна. Бозоны составляют один из двух классов частицы, другое существо фермионы.[229]
- Энтропия Браунштейна-Гоша-Северини: Это моделирование энтропии с использованием теории сетей используется при анализе квантовая гравитация и назван в честь Сибасиша Гхоша и его товарищей по команде, Сэмюэл Л. Браунштейн и Симоне Северини.
- Предел Чандрасекара и Число Чандрасекара: Обнаружен и назван в честь Субраманян Чандрасекар, получивший Нобелевская премия по физике в 1983 году за работу над звездная структура и звездная эволюция.[230] Субррахманян Чандрасекар открыл расчет, используемый для определения будущего того, что произойдет с умирающей звездой. Если масса звезды меньше предела Чандрасекара, она сожмется, превратившись в белый карлик, а если она велика, звезда взорвется, превратившись в сверхновую.
- Галенит, прикладное использование в электронике: Бенгальский ученый Сэр Джагадиш Чандра Босе эффективно использовал кристаллы галенита для построения радиоприемников.[231] Приемники Galena компании Bose использовались для приема сигналов, состоящих из коротковолновый, белый свет и ультрафиолетовый свет.[231] В 1904 году Бозе запатентовал использование детектора галенита, который он назвал Точечный контактный диод с использованием Galena.[232]
- Гелий: Французский астроном, Пьер Янссен наблюдал солнечное затмение 18 августа 1868 года из Гунтура в штате Мадрас, Британская Индия. Он обнаружил первое свидетельство гелия в виде ярко-желтой линии на хромографе Солнца.
- Расстояние Махаланобиса: Представлен в 1936 году индийским (бенгальским) статистиком. Прасанта Чандра Махаланобис (29 июня 1893 - 28 июня 1972), эта мера расстояния, основанная на корреляции между переменными, используется для выявления и анализа различающихся закономерностей по отношению к одной базе.[233]
- Ртутный нитрит: Соединение нитрита ртути было открыто в 1896 году бенгальским химиком Прафуллой Чандра Роем, который опубликовал свои открытия в Журнал Азиатского общества Бенгалии.[218] Это открытие послужило основой для значительных будущих исследований в области химии.[218]
- Рамачандран сюжет, Карта Рамачандрана и углы Рамачандрана: сюжет Рамачандрана и карта Рамачандрана были разработаны Гопаласамудрам Нараяна Айер Рамачандран, опубликовавший свои результаты в Журнал молекулярной биологии в 1963 году. Он также разработал углы Рамачандрана, которые служат удобным инструментом для коммуникация, представительство и различные виды анализ данных.[234]
- Рамановский эффект: Британская энциклопедия (2008) сообщает: «изменение длины волны света, которое происходит, когда световой луч отклоняется молекулами. Это явление названо в честь Сэр Чандрасекхара Венката Раман, открывший его в 1928 году. Когда луч света проходит через очищенный от пыли прозрачный образец химического соединения, небольшая часть света выходит в направлениях, отличных от направления падающего (входящего) луча. Большая часть этого рассеянного света имеет неизменную длину волны. Однако небольшая часть имеет длину волны, отличную от длины волны падающего света; его присутствие является результатом эффекта комбинационного рассеяния света ».[235]
- Уравнение Райчаудхури: Обнаружено Бенгальский физик Амаль Кумар Райчаудхури в 1954 году. Это был ключевой компонент Теоремы Пенроуза-Хокинга об особенностях из общая теория относительности.[236]
Космос
- Лунная вода: Хотя наличие водяного льда на Луне предполагалось различными учеными с 1960-х годов, были также обнаружены неубедительные доказательства наличия свободного водяного льда. Первым неопровержимым доказательством наличия воды на Луне был полезный груз "Чейс", который нес Зонд лунного удара выпущено Чандраяан-1 в 2009,[237][238][239] подтверждено и установлено НАСА.[240]
- Орбита Земли (Сидерический год ): Индуистский космологические циклы времени, объясненные в Сурья Сиддханта (около 600 г. н.э.), дайте среднюю длину звездного года (продолжительность обращения Земли вокруг Солнца) как 365,2563627 дней, что всего на 1,4 секунды больше, чем современное значение 365,256363004 дня.[241] Этот расчет был наиболее точной оценкой длины звездного года в любой точке мира за более чем тысячу лет.
- Периодичность комет: Индийские астрономы к 6 веку полагали, что кометы - это небесные тела, которые периодически появлялись снова. Так считали астрономы в VI веке. Варахамихира и Бхадрабаху, и астроном 10-го века Бхаттотпала перечислили названия и предполагаемые периоды некоторых комет, но, к сожалению, неизвестно, как эти цифры были рассчитаны и насколько они точны.[242]
- Уравнение ионизации Саха: Уравнение Саха, полученное бенгальским ученым. Мегнад Саха (6 октября 1893 - 16 февраля 1956) в 1920 г., концептуализирует ионизация в контексте звездных атмосфер.[243]
- Квазинормальные режимы из черные дыры: К. В. Вишвешвара обнаружил квазинормальные режимы черных дыр.[244] Эти моды колебаний черной дыры являются одной из основных целей наблюдения с помощью детекторов гравитационных волн.
Инновации
- Утюг рабочий: Металлургические заводы были разработаны в Индии примерно в то же время, но независимо от Анатолия и Кавказ. Археологические памятники в Индии, такие как Малхар, Дадупур, Раджа Нала Ка Тила и Лахурадева в наши дни Уттар-Прадеш показать железные орудия труда периода 1800–1200 гг. до н. э.[245] Ранние железные предметы, найденные в Индии, можно датировать 1400 г. до н. Э. С помощью метода радиоуглеродное датирование. Шипы, ножи, кинжалы, стрелка -головы, чаши, ложки, кастрюли, топоры, долота щипцы, дверная фурнитура и т. д. в пределах от 600 до 200 г. до н.э. были обнаружены на нескольких археологических раскопках Индии.[246] Некоторые ученые полагают, что к началу 13 века до н.э. выплавка железа в Индии была широко распространена, предполагая, что дата появления технологии может быть установлена раньше.[245] В Южная Индия (сегодняшний день Майсур ) железо появилось еще в 11-12 вв. до н. э .; эти события были слишком ранними для какого-либо значительного тесного контакта с северо-западом страны.[247] Во время Чандрагупта II Викрамадитья (375–413 гг. Н. Э.), Коррозионно-стойкое железо использовалось для возведения Железный столб Дели, которая выдерживает коррозию более 1600 лет.[248]
Информатика и программирование
- Симпьютер: Simputer (аббревиатура от «простой, недорогой и многоязычный компьютер для людей») - это автономный карманный компьютер с открытым аппаратным обеспечением, предназначенный для использования в средах, где вычислительные устройства, такие как персональные компьютеры, считаются неудобными. Он был разработан в 1999 году семью учеными Индийского института науки в Бангалоре под руководством доктора Свами Манохара в сотрудничестве с Encore India, компанией, базирующейся в Бангалоре.[249] Первоначально предполагалось, что Интернет станет доступным для масс Индии, Simputer и его производные сегодня широко используются правительствами нескольких индийских штатов в рамках своей инициативы электронного управления, индийской армией, а также другими государственными и частными организациями.
- Форма Бэкуса-Наура: В Информатика, Форма Бэкуса – Наура или же Бэкус нормальная форма (BNF) или же Форма Панини Бакуса[250] это техника записи за контекстно-свободные грамматики, часто используется для описания синтаксис из языки используется в вычислениях, таких как компьютер языки программирования, форматы документов, наборы инструкций и протоколы связи. Они применяются везде, где необходимы точные описания языков: например, в спецификациях официальных языков, в руководствах и в учебниках по теории языков программирования. Идея описания структуры языка с помощью правил переписывания может быть прослежена, по крайней мере, к работе из Панини (который жил где-то между 7 и 4 веками До н.э. ).[251][252] Название Форма Панини Бэкуса также было предложено ввиду того факта, что расширение Бэкус нормальная форма может быть неточным, и что Панини ранее независимо разработали аналогичные обозначения.[253] Его обозначения для описания санскрит нотация структуры слов эквивалентна по мощности нотации Бэкуса и имеет много схожих свойств.
Лингвистика
- Формальная грамматика: В его трактате Astadhyayi, Панини дает формальные производственные правила и определения для описания формальной грамматики санскрит.[254] В формальная теория языка, а грамматика (когда контекст не указан, часто называется формальная грамматика для наглядности) представляет собой набор правила производства за струны в формальный язык. Правила описывают, как формировать строки из языковых алфавит которые действительны в соответствии с языком синтаксис. Грамматика не описывает значение строк или что с ними можно сделать в любом контексте - только в их форме.
Метрология
- Стандартизация: Самые старые приложения и свидетельства стандартизации пришли из цивилизации долины Инда в 5-м тысячелетии до нашей эры.[11] характеризуется наличием гирь в различных стандартах и категориях, как[255] а также использование торговцами Инда централизованной системы мер и весов. Маленькие гири использовались для измерения предметов роскоши, а гири большего размера использовались для покупки более объемных предметов, таких как зерно и т. Д.[255] Веса и меры цивилизации Инда также достигли Персия и Центральная Азия, где они были доработаны.[256]
В общей сложности 558 гирь было извлечено из Мохенджодаро, Хараппы и Чанху-даро, не считая дефектных грузов. Они не обнаружили статистически значимых различий между массами, извлеченными из пяти разных слоев, каждый толщиной около 1,5 м. Это было доказательством того, что строгий контроль существовал, по крайней мере, в течение 500-летнего периода. Гиря 13,7 г, по-видимому, является одной из единиц, используемых в долине Инда. Обозначения основаны на двоичный и десятичный системы. 83% гирь, которые были выкопаны из трех вышеуказанных городов, были кубическими, а 68% были сделаны из черт.[11]
- Технические стандарты: Технические стандарты применялись и использовались в Цивилизация долины Инда с 5-го тысячелетия до нашей эры, чтобы измерительные приборы могли эффективно использоваться в угловое измерение и измерение в разработке.[257] Единые единицы длины использовались при планировании и строительстве городов, таких как Лотал, Суркотада, Калибанган, Дхолавира, Хараппа, и Мохенджо-Даро.[11] Веса и меры цивилизации Инда также достигли Персия и Центральная Азия, где они были доработаны.[256] Шигео Ивата описывает выкопанные гири, обнаруженные в цивилизации Инда:
Смотрите также
- Хронология индийских инноваций
- Университет Наланды
- История науки и техники в Индии
- Хронология исторических изобретений
Рекомендации
- ^ Нанда, Мира (16 сентября 2016 г.), "Зависть хиндутвы к науке", Линия фронта, получено 14 октября 2016
- ^ Баласубраманиам, Р. (2002)
- ^ Васеда, Йошио; Сигэру Сузуки (2006). Определение характеристик продуктов коррозии на стальных поверхностях. Pg.vii. ISBN 978-3-540-35177-1. Получено 27 мая 2009.
- ^ а б c d Ливингстон и Бич, 20
- ^ Затерянная река Мишеля Данино. Пингвин Индия 2010
- ^ а б Ливингстон и пляж, стр. Xxiii
- ^ а б c Британская энциклопедия (2008). Пагода.
- ^ Родда, Дж. К. и Убертини, Лучио (2004). Основа цивилизации - наука о воде? стр. 161. Международная ассоциация гидрологических наук (Международная ассоциация гидрологических наук Press 2004).
- ^ а б Whitelaw, страница 14
- ^ Whitelaw, страница 15
- ^ а б c d е Ивата, 2254 г.
- ^ Петрусо, Карл М (1981). ""Ранние веса и взвешивание в Египте и долине Инда ", Бюллетень М". Бюллетень M (Музей изящных искусств, Бостон). Бостонский музей изящных искусств. 79: 44–51. JSTOR 4171634.
- ^ "Исследование Джагадиса Боса по измерению роста растений". Получено 5 августа 2008.
- ^ Геддес, страницы 173–176
- ^ а б c Шафер (1963), страницы 160–161
- ^ а б c Бедини (1994), стр. 69–80.
- ^ Бедини (1994), стр.25
- ^ Зайверт (2003), стр.96
- ^ Кумар, Юктешвар (2005), стр. 65
- ^ а б Джулефф, Г. (1996). «Древняя ветровая технология выплавки чугуна в Шри-Ланке». Природа. 379 (6560): 60–63. Bibcode:1996 Натур 379 ... 60 Дж. Дои:10.1038 / 379060a0. S2CID 205026185.
- ^ "WOOTZ STEEL: ДОПОЛНИТЕЛЬНЫЙ МАТЕРИАЛ ДРЕВНЕГО МИРА". материалы.iisc.ernet.in. Архивировано из оригинал 11 февраля 2019 г.. Получено 23 июля 2008.
- ^ Шринивасан 1994
- ^ Шринивасан и Гриффитс
- ^ "Индийский журнал истории и науки, 34 (4), 1999 (через" Цифровую библиотеку Индии ")" (PDF). dli.gov.in. Архивировано из оригинал (PDF) 23 сентября 2015 г.. Получено 13 апреля 2015.
- ^ «Великое прошлое в ярких красках». Линия фронта. Индия. 8 октября 2010 г. Архивировано с оригинал 3 февраля 2011 г.
- ^ «Рис. 7. Два дамасских меча и отметины на поверхности». www.researchgate.net.
- ^ Камарустафа (1992), стр. 48
- ^ а б Сэвидж-Смит, Эмили (1985). Исламизировать небесные глобусы: их история, конструкция и использование. Smithsonian Institution Press, Вашингтон, округ Колумбия
- ^ Вуд, Мэрили; Дюссюбье, Лор; Робертшоу, Питер (1 июня 2012 г.). «Стакан чибуене, Мозамбик: новые взгляды на торговлю в Индийском океане». Южноафриканский археологический бюллетень. 67: 59–74.
- ^ Вуд, Мэрили; Панигелло, Серена; Орсега, Эмилио Ф .; Робертшоу, Питер; ван Элтерен, Йоханнес Т .; Кроутер, Элисон; Хортон, Марк; Бойвин, Николь (2017). «Торговля Занзибаром и Индийским океаном в первом тысячелетии нашей эры: свидетельство стеклянных бусинок». Археологические и антропологические науки. 9 (5): 879–901. Дои:10.1007 / s12520-015-0310-z. ISSN 1866-9557. S2CID 49586474.
- ^ Вуд, Мэрили (2012). «Взаимосвязи: стеклянные бусы и торговля в южной и восточной Африке и Индийском океане - 7-16 века нашей эры». Азания: археологические исследования в Африке. 47 (2): 248. Дои:10.1080 / 0067270X.2012.680307. ISSN 0067-270X. S2CID 162211326.
- ^ Кенойер, Видале, Дж. М., Массимо (май 1992 г.). «Новый взгляд на каменные сверла в традициях долины Инда» (PDF). РАБОТА СИМПОЗИУМА ОБЩЕСТВА ИССЛЕДОВАНИЙ ПО МАТЕРИАЛАМ. 267: 495–518. Дои:10.1557 / PROC-267-495.
- ^ а б Гвиннетт, А. Джон; Горелик, Леонард (1991). «Производство бисера в Хаджар Ар-Райхани, Йемен». Библейский археолог. 54 (4): 187–196. Дои:10.2307/3210280. ISSN 0006-0895. JSTOR 3210280.
- ^ Гвиннетт, А. Джон; Горелик, Л. (1993). «Бусы, скарабеи и амулеты: способы изготовления в Древнем Египте». Журнал Американского исследовательского центра в Египте. 30: 125–132. Дои:10.2307/40000232. ISSN 0065-9991. JSTOR 40000232.
- ^ «Разработка политических моделей в приморской Юго-Восточной Азии и пан-региональной культуры: вклад исследования системы ремесел каменных украшений Као Сек». ResearchGate. Получено 11 мая 2020.
- ^ Кин, Мануэль (1981). «ЛАПИДАРНОЕ ИСКУССТВО В ИСЛАМЕ». Penn Museum. Получено 31 июля 2020.
- ^ С Прасанна, Microsoft VJ # .Net производится в Индии. В архиве 28 ноября 2013 г. Wayback Machine, Экспресс Компьютер, 29 июля 2002 г. - недействительная ссылка!
- ^ «Линия бизнеса Hindu: Microsoft выстраивает большие планы в отношении центра в Хайдарабаде». www.thehindubusinessline.com.
- ^ "Домашняя страница Коджо". Получено 29 августа 2012.
- ^ Гирджан Веленга (19 февраля 2010 г.). «Интервью: среда обучения Scala на платформе NetBeans». DZone. Получено 29 августа 2012.
- ^ Б. Б. Лал, Индия, 1947–1997 гг .: новый взгляд на цивилизацию Инда
- ^ а б Банержи, стр. 673
- ^ Готцеген, стр.30.
- ^ Смит, Дж. А. (1992), стр. 23
- ^ "Индийские туши", Британская энциклопедия, 2008
- ^ Sircar, стр.206
- ^ Sircar, стр.62
- ^ Sircar, стр.67
- ^ «Известные ученые - Джагдиш Чандра Бозе». humantouchofchemistry.com. Архивировано из оригинал 18 ноября 2015 г.. Получено 5 января 2016.
- ^ «15 индийских изобретений и открытий, которые сформировали современный мир - Часть 2». The Huffington Post.
- ^ «Определение интерферометра Мурти». Photonics.com.
- ^ Riley, M.E .; Гусинов, М.А. (1 октября 1977 г.). «Расходимость лазерного луча с использованием интерферометра бокового сдвига». Прикладная оптика. 16 (10): 2753–6. Bibcode:1977ApOpt..16.2753R. Дои:10.1364 / AO.16.002753. PMID 20174226.
- ^ Роддам Нарасимха (1985), Ракеты в Майсоре и Британии, 1750–1850 гг. Н. Э. В архиве 27 сентября 2007 г. Wayback Machine, Национальная аэронавигационная лаборатория и Индийский институт науки "Хайдер Али, принц Майсура, разработал боевые ракеты с важным изменением: использование металлических цилиндров для хранения пороха. Хотя кованое мягкое железо, которое он использовал, было грубым, прочность на разрыв контейнер с черным порохом был намного выше, чем раньше, бумажная конструкция. Таким образом, было возможно более высокое внутреннее давление и, как следствие, большая тяга движущей струи. Корпус ракеты был привязан кожаными ремнями к длинной бамбуковой палке. до трех четвертей мили (более километра). Хотя по отдельности эти ракеты не были точными, ошибка рассеивания становилась менее важной, когда большое количество выпускалось быстро в массовых атаках. Они были особенно эффективны против кавалерии и были подброшены в воздух. после освещения или скользил по твердой сухой земле. Сын Хайдера Али, Типпу Султан, продолжала разрабатывать и расширять применение ракетного оружия, увеличив, по сообщениям, численность ракетных войск с 1200 до 5000 корпусов. В боях при Серингапатам в 1792 и 1799 годах эти ракеты со значительным успехом использовались против британцев »- Encyclopædia Britannica (2008). ракета и ракета.
- ^ чампо (चाँपो [tʃãpoː]) это императив из чампна (चाँपना [tʃãːpnaː]), «намазать, размять мышцы, помассировать голову и волосы»
- ^ Дуглас Харпер. «Интернет-этимологический словарь». Получено 14 июля 2007.
- ^ kSuNa, Санскритский лексикон, Словарь Монье-Вильямса (1872 г.)
- ^ фенака, Разговорный санскрит, Кельнский университет, Германия
- ^ Рахман, История индийской науки, техники и культуры в Google Книги, Издательство Оксфордского университета, ISBN 978-0195646528, стр.145
- ^ Совет по лекарственным растениям Тамил Наду В архиве 21 июля 2011 г. Wayback Machine
- ^ Сельскохозяйственный университет Тамил Наду - Albizzia amara
- ^ Хушвант Сингх, Гимны Гуру Нанака, Восточный Лонгман, ISBN 978-8125011613
- ^ Вирджиния Смит (2007 г.), Чистота: история личной гигиены и чистоты, Oxford University Press, ISBN 978-0199297795
- ^ Чемберлин (2007), стр. 80
- ^ а б Хобсон (2004), стр.103
- ^ а б c d Woods & Woods (2000), страницы 52–53.
- ^ «16.17.4: Стремена». Энциклопедия индийской археологии (Том 1). Отредактировал Амалананда Гош (1990). стр. 336
- ^ Аззароли (1985), стр.156
- ^ а б Аддингтон (1990), стр. 45
- ^ а б Баруа (2005), страницы 16–17.
- ^ Чакрабарти, Ананда М. (1981). «Микроорганизмы, имеющие несколько совместимых плазмид, генерирующих энергию разложения, и их получение».
- ^ Чакрабарти, AM; Mylroie, JR; Friello, DA; Вакка, Дж. Г. (1975). «Трансформация Pseudomonas putida и Escherichia coli с плазмидной ДНК фактора устойчивости к лекарствам». Труды Национальной академии наук Соединенных Штатов Америки. 72 (9): 3647–51. Bibcode:1975PNAS ... 72.3647C. Дои:10.1073 / pnas.72.9.3647. ЧВК 433053. PMID 1103151.
- ^ Чакрабарти, AM; Фрилло, Д.А. (1974). «Диссоциация и взаимодействие отдельных компонентов агрегата деградационной плазмиды у Pseudomonas». Труды Национальной академии наук Соединенных Штатов Америки. 71 (9): 3410–4. Bibcode:1974PNAS ... 71.3410C. Дои:10.1073 / пнас.71.9.3410. ЧВК 433782. PMID 4530312.
- ^ Чакрабарти, AM (1974). «Диссоциация деградирующего агрегата плазмиды у Pseudomonas». Журнал бактериологии. 118 (3): 815–20. Дои:10.1128 / JB.118.3.815-820.1974. ЧВК 246827. PMID 4829926.
- ^ Чакрабарти, AM (1974). «Транскрипционный контроль экспрессии деградационной плазмиды в Pseudomonas». Контроль транскрипции. Основные науки о жизни. 3. С. 157–65. Дои:10.1007/978-1-4613-4529-9_13. ISBN 978-1-4613-4531-2. PMID 4823075.
- ^ Шахам, М; Чакрабарти, AM; Гунсалус, IC (1973). «Перенос хромосом, опосредованный камфорной плазмидой в Pseudomonas putida». Журнал бактериологии. 116 (2): 944–9. Дои:10.1128 / JB.116.2.944-949.1973. ЧВК 285467. PMID 4745436.
- ^ Rheinwald, JG; Чакрабарти, AM; Гунсалус, IC (1973). «Трансмиссивная плазмида, контролирующая окисление камфоры у Pseudomonas putida». Труды Национальной академии наук Соединенных Штатов Америки. 70 (3): 885–9. Bibcode:1973ПНАС ... 70..885Р. Дои:10.1073 / пнас.70.3.885. ЧВК 433381. PMID 4351810.
- ^ "Окружающая среда: жук, поедающий масло". Время. 22 сентября 1975 г.. Получено 28 сентября 2009.
- ^ "Даймонд против Чакрабарти 447 U.S. 303 (1980)". Закон справедливости.
- ^ Мюррей (1913)
- ^ Форбс (1860)
- ^ а б Джонс, Уильям (1807). «Об индийской игре в шахматы». страницы 323–333
- ^ Линде, Антониус (1981)
- ^ Уилкинсон, Чарльз К. (май 1943 г.)
- ^ Птица (1893), стр. 63
- ^ Хупер и Уилд (1992), стр. 74
- ^ Сапра, Рахул (2000). «Спорт в Индии». Студенческая Британника Индии (Том 6). Мумбаи: популярный Пракашан. п. 106. ISBN 0-85229-762-9.
- ^ а б Мери (2005), стр.148
- ^ а б Бэшем (2001), стр. 208
- ^ а б c Британская энциклопедия (2002). Шахматы: древние предшественники и похожие игры.
- ^ Британская энциклопедия (2007). Шахматы: знакомство с Европой.
- ^ а б Альтер, стр.88
- ^ а б c MSN Encarta (2008). Пачиси.
- ^ а б Августин, страницы 27–28.
- ^ а б Джеймс Макманус (27 октября 2009 г.). Cowboys Full: История покера. Макмиллан. п. 34. ISBN 978-0-374-29924-8.
- ^ Карлайл, Родни (2009), Энциклопедия игры в современном обществе, Публикации SAGE, п. 31, ISBN 978-1-4129-6670-2
- ^ Quackenbos (2010), Иллюстрированная история древней литературы, восточной и классической литературы, ЧИТАТЬ КНИГИ, стр. 60, ISBN 978-1-4455-7978-8
- ^ Капур, Субодх (2002), Индийская энциклопедия: биографическая, историческая, религиозная, административная, этнологическая, коммерческая и научная - Том 6, Genesis Publishing Pvt Ltd, стр. 1786 г., ISBN 978-81-7755-257-7
- ^ Таунсенд, Джордж (1862), Справочник дат: справочник всех важнейших событий в истории человечества, которые можно найти в достоверных записях., Рутледж, Уорн и Рутледж, стр. 184
- ^ Нидхэм, Джозеф (2004). Наука и цивилизация в Китае. V: 1. Издательство Кембриджского университета. С. 131–132. ISBN 978-0-521-05802-5.
- ^ Дэвид Г. Шварц (5 октября 2006 г.). Roll the bone: история азартных игр. Книги Готэма. ISBN 978-1-59240-208-3.
- ^ а б Гессе, Райнер В. и Гессе (мл.), Райнер В. (2007). История ювелирного дела: энциклопедия. Издательская группа "Гринвуд". 35. ISBN 0-313-33507-9.
- ^ Макнил, Ян (1990). Энциклопедия истории техники. Тейлор и Фрэнсис. 852. ISBN 0-415-01306-2.
- ^ а б c d Британская энциклопедия (2008). ситцевая ткань
- ^ а б c d Бабер (1996), стр. 57
- ^ Смит, К. Уэйн; Котрен, Дж. Том (1999). Хлопок: происхождение, история, технология и производство. 4. Джон Вили и сыновья. стр. viii. ISBN 978-0471180456.
Первым усовершенствованием технологии прядения было прялочное колесо, которое было изобретено в Индии между 500 и 1000 годами нашей эры.
- ^ а б Британская энциклопедия (2008). ситец
- ^ Hāṇḍā (1998), стр. 133
- ^ Карим, Абдул (2012). «Муслин». В Ислам, Сираджул; Джамал, Ахмед А. (ред.). Банглапедия: Национальная энциклопедия Бангладеш (Второе изд.). Азиатское общество Бангладеш.
- ^ а б Ахмад, С. (июль – сентябрь 2005 г.). «Взлет и падение экономики Бенгалии». По делам Азии. 27 (3): 5–26.
- ^ Британская энциклопедия (2008). дизайн интерьера
- ^ а б Британская энциклопедия (2008). бригада
- ^ а б Британская энциклопедия (2008). квилтинг
- ^ а б Баркер, стр.13
- ^ а б Пиво, страница 60
- ^ а б Мудрый, стр. 11–12
- ^ Анжела Лаквете: Изобретение хлопкоочистителя: машина и миф в довоенной Америке, Издательство Университета Джона Хопкинса, 2003 г., ISBN 0-8018-7394-0, п. 5
- ^ Бабер (1996), стр. 56
- ^ а б c Тодд, Янв (1995). От Майло до Майло: история гантелей, гантелей и индийских булав. Проверено в сентябре 2008 г. Размещено на Спортивная библиотека фонда LA84.
- ^ "настоящий изобретатель" (PDF).
- ^ Декарт, Рене (2006). Размышления первой философии. ReadHowYouWant.com, Limited. ISBN 978-1-4250-0922-9.
- ^ Британская энциклопедия (2008). кашемир.
- ^ а б Британская энциклопедия (2008). кашмирский платок.
- ^ Штейн (1998), стр. 47
- ^ Wisseman & Williams (1994), стр.127
- ^ Энциклопедия Колумбии, шестое издание. хлопок.
- ^ а б c Кригер и Конна (2006), стр. 120
- ^ а б c d Британская энциклопедия (2008). джут.
- ^ а б Кеннет Кипл и Кримхильд Кони Орнелас. «Всемирная история еды - сахара». Издательство Кембриджского университета. Получено 9 января 2012.
- ^ Адас (2001), стр. 311
- ^ а б Кешник (2003)
- ^ а б Кешник (2003), стр. 258
- ^ Нильс-Бертил Валлин (19 ноября 2002 г.). «История нуля». Йельский центр изучения глобализации. Архивировано из оригинал 25 августа 2016 г.. Получено 26 декабря 2011.
- ^ Доктор Хоссейн Аршам. «Ноль в четырех измерениях». Университет Балтимора. Получено 26 декабря 2011.
- ^ Девлин, Ханна (13 сентября 2017 г.). «Много шума из ничего: древнеиндийский текст содержит самый ранний нулевой символ». Хранитель. ISSN 0261-3077. Получено 14 сентября 2017.
- ^ Смит, Дэвид Юджин (1958). История математики. Courier Dover Publications. п. 280. ISBN 978-0-486-20429-1.
- ^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф., «Шридхара», Архив истории математики MacTutor, Сент-Эндрюсский университет.
- ^ Crandall & Pomerance (2005), страницы 200–201.
- ^ а б Вайсштейн, Эрик В. «Тест на первичность АКС». MathWorld.
- ^ Крэндалл и Пападопулос (2003), стр.2
- ^ Ван Браммелен, Глен (2009). Математика неба и земли: ранняя история тригонометрии. Издательство Принстонского университета. п. 329. ISBN 9780691129730. (стр.111)
- ^ Мейеринг, Эрик (март 2002 г.). «Хронология интерполяции от древней астрономии до современной обработки сигналов и изображений». Труды IEEE. 90 (3): 319–342. Дои:10.1109/5.993400.
- ^ Гупта, Р. К. "Интерполяция второго порядка в индийской математике до пятнадцатого века". Индийский журнал истории науки. 4 (1 & 2): 86–98.
- ^ а б c d е ж грамм час я j Белл (1992), стр.96
- ^ Нитис (2000), стр. 325
- ^ Боос и Оливер (1998)
- ^ R.C. Гупта, Энциклопедия истории науки, техники и медицины в незападных культурах, п. 156.
- ^ Раджу, С.К. (2009), «Косамби-математик», Экономический и политический еженедельник, 44 (20): 33–45
- ^ Косамби, Д. Д. (1943), "Статистика в функциональном пространстве", Журнал Индийского математического общества, 7: 76–88, МИСТЕР 0009816.
- ^ Plofker (2007), стр. 419–436.
- ^ Джозеф (2000), стр.306
- ^ Кала Фишбейн, Тэмми Брукс. «Формула Брахмагупты». Университет Джорджии. Получено 3 ноября 2011.
- ^ Вайсштейн, Эрик В. «Матрица Брахмагупты». Mathworld. Получено 3 ноября 2011.
- ^ а б «Бхаскарачарья II». Энциклопедия студентов Индии (2000). (Том 1: Адб Аллах ибн аль Аббас - Кипарис). п. 200. ISBN 0-85229-760-2
- ^ Кумар (2004), стр.23
- ^ Сингх, Манпал (2005), стр. 385
- ^ Плофкер (2007), стр. 474
- ^ а б c Goonatilake (1998), стр.127 - 128
- ^ Бабер (1996), стр. 34
- ^ Рао К. А. (2000), стр. 252
- ^ «Индийские цифры». www-history.mcs.st-and.ac.uk. Получено 13 апреля 2015.
- ^ Саломон, Р. (1998). Индийская эпиграфия: руководство по изучению надписей на санскрите, пракрите и других индоарийских языках. Oxford University Press, США. п. 61. ISBN 9780195099843. Получено 13 апреля 2015.
- ^ Реймер, Л., Реймер, В. Математики тоже люди: Истории из жизни великих математиков, Vol. 2. 1995. С. 22–22. Парсиппани, Нью-Джерси: Pearson Education, Inc. как Dale Seymor Publications. ISBN 0-86651-823-1.
- ^ Гунатилаке, С. (1998). На пути к глобальной науке: добыча цивилизационных знаний. Издательство Индианского университета. п.126. ISBN 9780253333889. Получено 13 апреля 2015.
- ^ а б c Смит (1958), стр. 257–258.
- ^ а б Бурбаки (1998), стр. 49
- ^ Краткая энциклопедия Британики (2007). алгебра
- ^ а б Goonatilake (1998), стр. 37
- ^ Амма (1999), стр. 182–183.
- ^ а б Рой (1990)
- ^ Борвейн (2004), стр. 107
- ^ Плофкер (2007), стр. 481
- ^ Брессуд (2002)
- ^ Плофкер (2001)
- ^ Кац (1995)
- ^ а б "Биография Варахамихира". www-history.mcs.st-andrews.ac.uk. Получено 13 апреля 2015.
- ^ Эдвардс, A.W.F. (2002). Арифметический треугольник Паскаля: история математической идеи. Издательство Университета Джона Хопкинса. п. 201. ISBN 9780801869464. Получено 13 апреля 2015.
- ^ Путтасвами (2000), стр. 416
- ^ а б Stillwell (2004), страницы 72–73.
- ^ Берндт и Рэнкин (2001)
- ^ Белл (1992), стр.97
- ^ "Биография Аль-Кинди". www-gap.dcs.st-and.ac.uk. Архивировано из оригинал 26 октября 2007 г.
- ^ Пингри (2003):
"Геометрия и ее ветвь тригонометрии были математикой, которую индийские астрономы использовали наиболее часто. Фактически, индийские астрономы в третьем или четвертом веке, используя доптолемеевскую греческую таблицу аккордов, составили таблицы синусов и версин, из которых она было тривиально вывести косинусы. Эта новая система тригонометрии, созданная в Индии, была передана арабам в конце восьмого века, а ими в расширенной форме - латинскому Западу и византийскому Востоку в двенадцатом веке ».
- ^ Дж. Дж. О'Коннор и Э. Ф. Робертсон (1996). Тригонометрические функции В архиве 24 сентября 2012 в WebCite. Архив истории математики MacTutor
- ^ Зыск, К. Г. (1991). Аскетизм и исцеление. Лондон, Нью-Йорк, Дели: Издательство Оксфордского университета. ISBN 978-0-19-505956-4.
- ^ Чопра 2003, п. 75
- ^ Звелебил, Камиль В. (1996). Сиддха в поисках бессмертия. Оксфорд: Мандрагора Оксфорда. ISBN 978-1-869928-43-8.
- ^ Шарф, Хартмут (1999). «Доктрина трех юморов в традиционной индийской медицине и предполагаемая древность тамильской медицины сиддхов». Журнал Американского восточного общества. 119 (4): 609–629. Дои:10.2307/604837. JSTOR 604837.
- ^ Дешпанде, Виджая (2000). «Офтальмологическая хирургия: глава в истории китайско-индийских медицинских контактов». Вестник школы востоковедения и африканистики. 63 (3): 370. Дои:10.1017 / s0041977x00008454.
- ^ а б c d Палец (2001), стр.66
- ^ Ладе и Свобода (2000), стр. 85
- ^ Кирнс и Нэш (2008)
- ^ Замок; Last & Dunea (2001), стр. 420
- ^ Шиффман, Мелвин (5 сентября 2012 г.). Косметическая хирургия: искусство и методы. Springer. п. 20. ISBN 978-3-642-21837-8.
- ^ Mazzola, Ricardo F .; Маццола, Изабелла К. (5 сентября 2012 г.). Пластическая хирургия: принципы. Elsevier Health Sciences. С. 11–12. ISBN 978-1-4557-1052-2.
- ^ а б MSN Encarta (2008). Пластическая хирургия В архиве 22 сентября 2008 г. Wayback Machine.
- ^ а б Двиведи, Гириш; Двиведи, Шридхар (2007). «Сушрута - клиницист - превосходный учитель» (PDF). Индийский журнал болезней грудной клетки и смежных наук. 49: 243–4. Архивировано из оригинал (PDF) 10 октября 2008 г.
- ^ а б c Замок и т. Д., Стр. 607
- ^ а б Замок; Last & Dunea (2001), стр. 836
- ^ Нобелевский фонд (2008). База данных о номинациях на Нобелевскую премию по физиологии и медицине за 1901–1951 гг.
- ^ а б Упендра Натх Брахмачари: пионер современной медицины в Индии. Вигьян Прасар: Правительство Индии
- ^ а б c d е Дикинсон, страницы 1–3
- ^ Херши (2004), стр.22
- ^ Малкин (1996), стр.12
- ^ Херши (2004), страницы 3 и 23
- ^ Томас (2007), стр. 46
- ^ Читать (2005), стр.17
- ^ а б Ли, стр. 685
- ^ а б Венк, страницы 535–539.
- ^ MSN Encarta (2007). Алмаз. В архиве 1 ноября 2009 г.
- ^ "Цинк-Информационный бюллетень". Австралийские шахты. Архивировано из оригинал 7 ноября 2011 г.. Получено 4 ноября 2011.
- ^ Шринивасан, Ранганатан. «Металлургическое наследие Индии». Кристиан-Альбрехтский университет Киля. Получено 4 ноября 2011.
- ^ Рина Шриваства (1999). «Плавильные печи в Древней Индии» (PDF). Индийский журнал истории и науки, 34 (1), Цифровая библиотека Индии. Архивировано из оригинал (PDF) 25 апреля 2012 г.. Получено 4 ноября 2011.
- ^ а б Крэддок (1983)
- ^ Бисвас (1986), стр.11
- ^ Пиковер, Клиффорд (16 апреля 2008 г.). От Архимеда до Хокинга: законы науки и великие умы, стоящие за ними. Издательство Оксфордского университета. ISBN 9780199792689.
- ^ Бозе, Майнак Кумар (1988). Поздняя классическая Индия. A. Mukherjee & Co.
- ^ *Сен, Амартия (2005). Аргументативный индеец. Аллен Лейн. п. 29. ISBN 978-0-7139-9687-6.
- ^ а б c d «Ачарья Прафулла Чандра Рэй» В архиве 27 сентября 2007 г. Wayback Machine, Виян Прасар, Департамент науки и технологий, правительство Индии.
- ^ а б Шанти Сваруп Бхатнагар В архиве 18 октября 2013 г. Wayback Machine. Вигьян Прасар: Правительство Индии.
- ^ а б Пенни (1967), стр. 39
- ^ а б c Ригден (2005), страницы 143–144.
- ^ а б c Фрейзер (2006), стр. 238
- ^ Доксуа и Пейрар (2006), страницы 297–298.
- ^ Заметки к лекции Дирака Развитие атомной теории в Le Palais de la Découverte, 6 декабря 1945 г., UKNATARCHI Dirac Papers BW83 / 2/257889. См. Примечание 64 к стр. 331 в "Самом странном человеке" Грэма Фармело
- ^ Дейгл, Кэти (10 июля 2012 г.). «Индия: хватит о Хиггсе, давайте обсудим бозон». AP Новости. Получено 10 июля 2012.
- ^ Бал, Хартош Сингх (19 сентября 2012 г.). "Бозе в бозоне". Нью-Йорк Таймс блог. Получено 21 сентября 2012.
- ^ Уэллс, Джон С. (1990). Словарь произношения longman. Харлоу, Англия: Лонгман. ISBN 978-0582053830. запись "Бозон"
- ^ "бозон". Словарь Коллинза.
- ^ Кэрролл, Шон (2007) Темная материя, темная энергия: темная сторона Вселенной, Путеводитель, часть 2 стр. 43, Учебная компания, ISBN 1598033506 "... бозон: частица, несущая силу, в отличие от частицы материи (фермиона). Бозоны могут быть наложены друг на друга без ограничений. Примеры включают фотоны, глюоны, гравитоны, слабые бозоны и бозон Хиггса. Спин бозона всегда целое число, например 0, 1, 2 и так далее ... "
- ^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. (Февраль 2005 г.), "Субраманян Чандрасекар", Архив истории математики MacTutor, Сент-Эндрюсский университет.
- ^ а б «Индийские ученые» (Ноябрь 2004 г.), Комитет по популяризации науки и работе с общественностью, Институт фундаментальных исследований Тата.
- ^ Саркар (2006), стр.94
- ^ Taguchi & Jugulum (2002), страницы 6–7.
- ^ Рамакришнан (2001)
- ^ «Рамановский эффект».Британская энциклопедия (2008)
- ^ Нареш (2005)
- ^ Репортер, сотрудники (25 сентября 2009 г.). «MIP обнаружила воду на Луне еще в июне: председатель ISRO». Индуистский.
- ^ «Индия победила НАСА в поиске воды на Луне?». m.ndtv.com. Архивировано из оригинал 30 ноября 2016 г.. Получено 29 ноябрь 2016.
- ^ "Чандраян-1 | Индийский космический зонд". Британская энциклопедия.
- ^ «Чандраян впервые обнаружил воду на Луне, но… | Последние новости и обновления в Daily News & Analysis». ДНК. 25 сентября 2009 г.
- ^ Уайт, М.Дж. «Сидерические, тропические и аномалистические годы» (PDF). Получено 16 мая 2016.
- ^ Келли, Дэвид Х .; Милоне, Юджин Ф. (2011). Изучение древнего неба: обзор древней и культурной астрономии. п. 293. ISBN 9781441976246.
- ^ Нарликар (2002), стр.188
- ^ Вишвешвара, C.V., Nature, 1970, 227, 936.
- ^ а б «Истоки обработки железа в Индии: новые свидетельства из равнины Центральной Ганги и Восточного Виндхья, написанные Ракешем Тевари (директор Государственного археологического департамента США)» (PDF). antiquity.ac.uk. Получено 13 апреля 2015.
- ^ Марко Чеккарелли (2000). Международный симпозиум по истории машин и механизмов: материалы симпозиума HMM. Springer. ISBN 0-7923-6372-8. стр. 218
- ^ И. М. Драконов (1991). Ранняя античность. Издательство Чикагского университета. ISBN 0-226-14465-8. стр. 372
- ^ Баласубраманиам, Р. (2000). "О коррозионной стойкости железной колонны Дели" (PDF). Наука о коррозии. 42 (12): 2103–29. Дои:10.1016 / s0010-938x (00) 00046-9.
- ^ "Simputer Definition из энциклопедии журнала PC". www.pcmag.com.
- ^ Ингерман, П. З. (1967). ""Форма Панини Бэкуса «предложена». Коммуникации ACM. 10 (3): 137. Дои:10.1145/363162.363165. S2CID 52817672.
- ^ "Биография Панини". Школа математики и статистики Университета Сент-Эндрюс, Шотландия. Получено 22 марта 2014.
- ^ Ингерман, Питер Зилахи (март 1967). ""Форма Панини-Бэкуса «Предлагаемая». Коммуникации ACM. 10 (3): 137. Дои:10.1145/363162.363165. S2CID 52817672. Ингерман предлагает переименовать нормальную форму Бэкуса в Панини -Backus Form, чтобы отдать должное Панини как первому независимому изобретателю.
- ^ Ингерман, П. З. (1967). ""Форма Панини Бэкуса «предложена». Коммуникации ACM. 10 (3): 137. Дои:10.1145/363162.363165. S2CID 52817672.
- ^ "Биография Панини". www-history.mcs.st-andrews.ac.uk.
- ^ а б Кенойер, 265
- ^ а б В третьем тысячелетии до нашей эры измерительная система Инд получила дальнейшее развитие в древних регионах Ирана и Афганистана - Ивата, 2254 г.
- ^ Бабер, 23 года
Библиография
- Адас, Майкл (январь 2001). Сельскохозяйственные и скотоводческие общества в древней и классической истории. Temple University Press. ISBN 1-56639-832-0.
- Аддингтон, Ларри Х. (1990). Образцы войны в восемнадцатом веке (Иллюстрированное издание). Индиана: Издательство Индианского университета. ISBN 0-253-20551-4.
- Альтер, Дж. С. в статье «Кабадди, национальный вид спорта Индии». Дайк, Ноэль (2000). Игры, спорт и культура. Издатели Berg: ISBN 1-85973-317-4.
- Амма, Т. А. Сарасвати (1999) [1979]. Геометрия в древней и средневековой Индии. Дели: Публикация Мотилала Банарсидасса. ISBN 81-208-1344-8.
- Аренсберг, Конрад М. и Нихофф, Артур Х. (1971). Введение в социальные изменения: руководство по развитию сообщества (второе издание). Нью-Джерси: Aldine Transaction. ISBN 0-202-01072-4
- Августин, Фредерик Дж. (2004). Словарь игрушек и игр в американской популярной культуре. Haworth Press. ISBN 0-7890-1504-8.
- Аззароли, Аугусто (1985). Ранняя история верховой езды. Массачусетс: издательство Brill Academic Publishers. ISBN 90-04-07233-0.
- Бабер, Захир (1996). Наука Империи: научные знания, цивилизация и колониальное правление в Индии. Государственный университет Нью-Йорка Press. ISBN 0-7914-2919-9.
- Сумка, А. К. (2005). «Фатхуллах Ширази: пушка, многоствольное ружье и яргу». Индийский журнал истории науки. 40 (3): 431–6.
- Баласубраманиам, Р. (2002). Железный столп Дели: новые идеи. Дели: Индийский институт перспективных исследований [Мичиганский университет]. ISBN 81-7305-223-9.
- Банерджи, Sures Chandra (1989). Сопровождение санскритской литературы. Motilal Banarsidass. ISBN 81-208-0063-Х.
- Баркер, Дайан (2003). Тибетские молитвенные флаги. Издательство Connections Book Publishing. ISBN 1-85906-106-0.
- Баруа, Прадип (2005). Государство в состоянии войны в Южной Азии. Небраска: University of Nebraska Press. ISBN 0-8032-1344-1.
- Башам, А.Л. (2001) [1967]. Чудо, которым была Индия. Третье исправленное издание. Нью-Дели: Rupa & co. ISBN 0-283-99257-3.
- Бедини, Сильвио А. (1994). След времени: измерение времени с помощью благовоний в Восточной Азии. Англия: Издательство Кембриджского университета. ISBN 0-521-37482-0.
- Белл, Эрик Темпл (1992). Развитие математики (первоначально опубликовано в 1945 году). Courier Dover Publications. ISBN 0-486-27239-7.
- Белл, Джон (2000). Струны, руки, тени: современная история кукол. Издательство Государственного университета Уэйна. ISBN 0-89558-156-6.
- Пиво, Роберт (2004). Энциклопедия тибетских символов и мотивов. Serindia Publications Inc. ISBN 1-932476-10-5.
- Птица, Генри Эдвард (1893). История шахмат и воспоминания. Лондон. (Переизданная версия Forgotten Books). ISBN 1-60620-897-7.
- Берндт, Брюс С .; Ранкин, Роберт Александр (2001). Рамануджан: очерки и опросы. Род-Айленд: Американское математическое общество. ISBN 978-0-8218-2624-9.
- Бисвас, Арун Кумар (Июнь 1986 г.). «Раса-Ратна-Самучкая и передовые технологии обработки минералов в 13 веке нашей эры, Индия» (PDF). Индийский журнал истории науки. 22 (1): 29–46. Архивировано из оригинал (PDF) 27 февраля 2009 г.. Получено 9 января 2009.
- Блехинден, Кэтлин (1905). Калькутта, прошлое и настоящее. Лос-Анджелес: Калифорнийский университет.
- Bondyopadhyay, Пробир К. (1988). "Диодный детектор сэра Дж. К. Бозе получил первый трансатлантический беспроводной сигнал Маркони в декабре 1901 года (повторение скандала с «когерером итальянского флота»)". Proc. IEEE, Vol. 86, No. 1, January 1988.
- Бога, Стивен (1996). Бадминтон. Пенсильвания: Stackpole Books. ISBN 0-8117-2487-5
- Боос, Деннис Д .; Оливер, Жаклин М. Хьюз (август 1998 г.). «Приложения теоремы Басу» (PDF). Американский статистик. 52 (3): 218–221. Дои:10.2307/2685927. JSTOR 2685927.
- Борвейн, Джонатан М. и Бейли, Дэвид Х. (2004) Математика экспериментально: правдоподобные рассуждения в 21 веке Массачусетс: А. К. Петерс, ООО ISBN 1-56881-211-6
- Бурбаки, Николас (1998). Элементы истории математики. Берлин, Гейдельберг и Нью-Йорк: Springer-Verlag. ISBN 3-540-64767-8.
- Брессуд, Дэвид (2002), «Исчисление изобретено в Индии?», Математический журнал колледжа (Математическая ассоциация Америки) 33 (1): 2–13
- Бродбент, Т. А. А .; Клайн, М. (октябрь 1968 г.). "Рецензированные работы: История древнеиндийской математики К. Н. Шринивасиенгара ". Математический вестник. 52 (381): 307–8. Дои:10.2307/3614212. JSTOR 3614212.
- Браун, У. Норман (1964). «Индийские игры в Пачиси, Чаупар и Чаусар». Экспедиция, 32–35. Музей археологии и антропологии Пенсильванского университета. 32 (35).
- Чемберлин, Дж. Эдвард (2007). Лошадь: как лошадь сформировала цивилизации. Москва: Olma Media Group. ISBN 1-904955-36-3.
- Чандра, Анджана Мотихар (2007). Краткое содержание Индии: 5000 лет истории и культуры Маршалл Кавендиш. ISBN 981-261-350-1
- Чопра, Ананда С. (2003). «Аюрведа». В Селин, Хелайн (ред.). Медицина в разных культурах: история и практика медицины в незападных культурах. Норуэлл, Массачусетс: Kluwer Academic Publishers. С. 75–83. ISBN 978-1-4020-1166-5.
- Двиведи, Гириш; Двиведи, Шридхар (2007). «История медицины: Сушрута - клиницист - превосходный учитель» (PDF). Индийский журнал болезней грудной клетки и смежных наук. Дели, Индия: Институт сундуков Валлаббхаи Пателя, Университет Дели / Национальный колледж грудных врачей. 49: 243–244. Архивировано из оригинал (PDF) 10 октября 2008 г. (Переиздано Национальный центр информатики, Правительство Индии.)
- Кук, Роджер (2005). История математики: краткий курс. Нью-Йорк: Wiley-Interscience. ISBN 0-471-44459-6.
- Коннорс, Мартин; Дюпюи, Дайан Л. и Морган, Брэд (1992). Сборник фактов об Олимпийских играх: Путеводитель по зимним и летним играм. Мичиган: Visible Ink Press. ISBN 0-8103-9417-0
- Coppa, A. et al. 2006. "Ранняя неолитическая традиция стоматологии ". Природа. Том 440. 6 апреля 2006 г.
- Крэддок, П. и другие. (1983). Производство цинка в средневековой Индии, Мировая археология, т. 15, нет. 2, Промышленная археология.
- Crandall, R. & Papadopoulos, J. (18 марта 2003 г.). "О реализации тестов на простоту класса AKS "
- Крэндалл, Ричард Э. и Померанс, Карл (2005). Простые числа: вычислительная перспектива (второе издание). Нью-Йорк: Спрингер. ISBN 0-387-25282-7.
- Дадхич, Нареш (август 2005 г.). «Амаль Кумар Райчаудхури (1923–2005)» (PDF). Текущая наука. 89 (3): 569–570.
- Дейлс, Джордж (1974). «Раскопки в Балакоте, Пакистан, 1973». Журнал полевой археологии. 1 (1–2): 3–22 [10]. Дои:10.2307/529703. JSTOR 529703.
- Дарьяи, Турадж (2006) в «Нарды» в Средневековая исламская цивилизация: энциклопедия изд. Мери, Йозеф В. и Бахарач, Джере Л., стр. 88–89. Тейлор и Фрэнсис.
- Доксуа, Тьерри и Пейрар, Мишель (2006). Физика солитонов. Англия: Издательство Кембриджского университета. ISBN 0-521-85421-0.
- Давре, Роберт (1978). «Таинственные города: Затерянная империя долины Инда». Последние тайны мира. (второе издание). Сидней: Ридерс Дайджест. ISBN 0-909486-61-1
- Дикинсон, Джоан Ю. (2001). Книга бриллиантов. Dover Publications. ISBN 0-486-41816-2.
- Древес, Ф. (2006). Генерация грамматических картинок: древовидный подход. Нью-Йорк: Спрингер. ISBN 3-540-21304-Х
- Дюрант, Уилл (1935). Наше восточное наследие. Нью-Йорк: Саймон и Шустер.
- Датфилд, Грэм (2003). Права интеллектуальной собственности и отрасли наук о жизни: история двадцатого века. Издательство Ashgate. ISBN 0-7546-2111-1.
- Двиведи, Гириш и Двиведи, Шридхар (2007). История медицины: Сушрута - клиницист - превосходный учитель. Национальный центр информатики (правительство Индии).
- Энциклопедия индийской археологии (Том 1). Отредактировал Амалананда Гош (1990). Массачусетс: издательство Brill Academic Publishers. ISBN 90-04-09264-1.
- Эмерсон, Д.Т. (1998).Работа Джагдиша Чандры Боса: 100 лет исследований миллиметровых волн. Национальная радиоастрономическая обсерватория.
- Эмсли, Джон (2003). Строительные блоки природы: руководство по элементам от А до Я. Англия: Издательство Оксфордского университета. ISBN 0-19-850340-7.
- Палец, Стэнли (2001). Истоки нейронауки: история исследований функций мозга. Англия: Издательство Оксфордского университета. ISBN 0-19-514694-8.
- Флегг, Грэм (2002). Числа: их история и значение. Courier Dover Publications. ISBN 0-486-42165-1.
- Форбс, Дункан (1860). История шахмат: со времени первого изобретения игры в Индии до периода ее становления в Западной и Центральной Европе. Лондон: W. H. Allen & co.
- Фаулер, Дэвид (1996). «Биномиальная функция коэффициента». Американский математический ежемесячник. 103 (1): 1–17. Дои:10.1080/00029890.1996.12004694. JSTOR 2975209.
- Фрейзер, Гордон (2006). Новая физика двадцать первого века. Англия: Издательство Кембриджского университета. ISBN 0-521-81600-9.
- Гангопадхьяя, Мриналканти (1980). Индийский атомизм: история и источники. Нью-Джерси: Humanities Press. ISBN 0-391-02177-X.
- Геддес, Патрик (2000). Жизнь и деятельность сэра Джагадиса К. Боса. Азиатские образовательные услуги. ISBN 81-206-1457-7.
- Гейер, Х. С. (2006), Глобальная регионализация: основные периферийные тенденции. Англия: Эдвард Элгар Паблишинг. ISBN 1-84376-905-0.
- Гхош, Амалананда (1990). Энциклопедия индийской археологии. Брилл. ISBN 90-04-09264-1.
- Ghosh, S .; Мэсси, Реджинальд; и Банерджи, Утпал Кумар (2006). Индийские куклы: прошлое, настоящее и будущее. Abhinav Publications. ISBN 81-7017-435-Х.
- Готцеген, Марк Э. (2006). Справочник художника: полный справочник. Нью-Йорк: публикации Watson-Guptill. ISBN 0-8230-3496-8.
- Goonatilake, Susantha (1998). На пути к глобальной науке: добыча цивилизационных знаний. Индиана: Издательство Индианского университета. ISBN 0-253-33388-1.
- Гийен, Жан-Ив (2004). Бадминтон: иллюстрированная история. Париж: Издания Publibook ISBN 2-7483-0572-8
- Хана, Омачанда (1998). Текстиль, костюмы и украшения Западных Гималаев. Indus Publishing. ISBN 81-7387-076-4.
- Хаяси, Такао (2005). Индийская математика во Флуде, Гэвин, Товарищ Блэквелла в индуизме, Oxford: Basil Blackwell, 616 страниц, стр. 360–375, 360–375, ISBN 978-1-4051-3251-0.
- Херши, Дж. Уиллард (2004). Книга алмазов: их любопытные знания, свойства, тесты и синтетическое производство 1940 Монтана: Kessinger Publishing. ISBN 1-4179-7715-9
- Хобсон, Джон М. (2004). Восточные истоки западной цивилизации (Иллюстрированное издание). Англия: Издательство Кембриджского университета. ISBN 0-521-54724-5.
- Хойберг, Дейл и Рамчандани, Инду (2000). Студенческая Британника Индия. Мумбаи: популярный Пракашан. ISBN 0-85229-760-2
- Хупер, Дэвид Винсент; Уилд, Кеннет (1992). Оксфордский товарищ по шахматам. Oxford University Press. ISBN 0-19-866164-9.
- Гувер, Герберт Кларк (2003). Георгиус Агрикола Де Ре Металлика Монтана: Kessinger Publishing. ISBN 0-7661-3197-1.
- Хопкинс, Дональд Р. (2002). Величайший убийца: оспа в истории. Издательство Чикагского университета. ISBN 0-226-35168-8.
- Ифра, Жорж (2000). Всеобщая история чисел: от предыстории до компьютеров. Нью-Йорк: Вили. ISBN 0-471-39340-1.
- Ингерман, П. З. (1967). «Предложена форма Панини-Бэкуса». Коммуникации ACM. 10 (3): 137. Дои:10.1145/363162.363165. S2CID 52817672.
- Ивата, Шигео (2008), «Меры и весы в долине Инда», Энциклопедия истории науки, техники и медицины в незападных культурах (2-е издание) Отредактировано Хелайн Селин, Springer, 2254–2255, ISBN 978-1-4020-4559-2.
- Джеймс, Джеффри (2003). Преодоление глобального цифрового разрыва. Cheltenham: Эдвард Элгар Паблишинг. ISBN 1-84376-206-4.
- Джонс, Уильям (1807). Работы сэра Уильяма Джонса (Том 4). Лондон.
- Джозеф, Джордж Гевергезе (2000). Гребень павлина: неевропейские корни математики. Принстон, штат Нью-Джерси: Princeton University Press. ISBN 0-691-00659-8.
- Таунсенд Уайт, Линн; Младший (1960). «Тибет, Индия и Малайя как источники западных средневековых технологий». Американский исторический обзор. 65 (3): 522–526. Дои:10.1086 / ahr / 65.3.515.
- Джулефф, Г. (1996). «Древняя ветровая технология выплавки чугуна в Шри-Ланке». Природа. 379 (6560): 60–63. Bibcode:1996 Натур 379 ... 60 Дж. Дои:10.1038 / 379060a0. S2CID 205026185.
- Камарустафа, Ахмет Т. (1992). «Часть 1 №1: Исламская картография 1». Картография в традиционных исламских и южноазиатских обществах. Vol. 2 Книга 1. Нью-Йорк: Издательство Оксфордского университета США. ISBN 0-226-31635-1
- Кац, В. Дж. (1995). «Идеи исчисления в исламе и Индии». Математический журнал. 68 (3): 163–174. Дои:10.2307/2691411. JSTOR 2691411.
- Кернс, Сюзанна С.Дж. и Нэш, Джун Э. (2008). проказа. Encyclopdia Britannica.
- Кешник, Джон (2003). Влияние буддизма на материальную культуру Китая. Нью-Джерси: Издательство Принстонского университета. ISBN 0-691-09676-7.
- Кипфер, Барбара Энн (2000). Энциклопедический словарь археологии. (Иллюстрированное издание). Нью-Йорк: Спрингер. ISBN 978-0-306-46158-3.
- Коппель, Том (2007). Приливы и отливы: приливы и отливы на нашей планете когда-то и в будущем. Dundurn Press Ltd. ISBN 1-55002-726-3.
- Кригер, Коллин Э. и Конна, Грэм (2006). Ткань в истории Западной Африки. Роуман Альтамира. ISBN 0-7591-0422-0.
- Кумар, Нарендра (2004). Наука в Древней Индии. Дели: Anmol Publications Pvt Ltd. ISBN 81-261-2056-8
- Кумар, Юктешвар (2005). История китайско-индийских отношений: 1 век - 7 век нашей эры. Нью-Дели: Издательство APH. ISBN 81-7648-798-8.
- Лейд, Арни и Свобода, Роберт (2000). Китайская медицина и аюрведа. Motilal Banarsidass. ISBN 81-208-1472-Х.
- Ли, Сонгю (2006). Энциклопедия химической обработки. CRC Press. ISBN 0-8247-5563-4.
- Линде, Антониус ван дер (1981) [1874] (на немецком языке). Geschichte und Literatur des Schachspiels. Цюрих: Издание Olms. ISBN 3-283-00079-4
- Ливингстон, Морна и Бич, Майло (2002). Шаги к воде: древние степные колодцы Индии. Princeton Architectural Press. ISBN 1-56898-324-7.
- Лок, Стивен; Наконец, Джон М .; Дунея, Джордж (2001). Oxford Illustrated Companion to Medicine. США: Издательство Оксфордского университета. ISBN 0-19-262950-6.
- Лоуи, Роберт Х. (2007) [1940]. Введение в культурную антропологию. Masterson Press. ISBN 1-4067-1765-7.
- Малкин, Стивен (1996). Технология шлифования: теория и применение абразивной обработки. Мичиган: Общество инженеров-производителей. ISBN 0-87263-480-9.
- МакЭвилли, Томас (2002). Форма древней мысли: сравнительные исследования греческой и индийской философий. Нью-Йорк: Allworth Communications Inc. ISBN 1-58115-203-5.
- Макинтош, Джейн (2007). Долина Древнего Инда: новые перспективы. Иллюстрированное издание. Калифорния: ABC-CLIO. ISBN 1-57607-907-4.
- Мери, Йозеф В. (2005). Средневековая исламская цивилизация: энциклопедия. Рутледж. ISBN 0-415-96690-6.
- Миллар, Стюарт (2004). «Использование технологий: карманные компьютеры преодолевают цифровой разрыв». Мир в движении: будущее, наука и технологии. Дания: Systime. С. 167–169. ISBN 87-616-0887-4
- Мюррей, Х. Дж. Р. (1913). История шахмат. Англия: Издательство Оксфордского университета.
- Нарликар, Дж. В. (2002). Введение в космологию. Издательство Кембриджского университета. ISBN 0-521-79376-9.
- Неджат, Карен Рея Немет. (1998). Повседневная жизнь в Древней Месопотамии. Коннектикут: Издательская группа Гринвуд. ISBN 0-313-29497-6.
- Нитис, Мухопадхьяй (2000). Вероятность и статистический вывод. Статистика: серия учебников и монографий. 162. Флорида: CRC Press USA. ISBN 0-8247-0379-0.
- Пейси, Арнольд (1991). Технологии в мировой цивилизации: тысячелетняя история. MIT Press. ISBN 0-262-66072-5.
- Пенни, лорд (Ноябрь 1967). "Хоми Джехангир Бхабха. 1909–1966". Биографические воспоминания членов Королевского общества. 13: 35–55. Дои:10.1098 / рсбм.1967.0002. JSTOR 769371.
- Пирси, У. Дуглас и Скарборо, Гарольд (2008). больница. Encyclopdia Britannica.
- Пингри, Дэвид (2003). «Логика незападной науки: математические открытия в средневековой Индии». Дедал. 132 (4): 45–54. Дои:10.1162/001152603771338779. S2CID 57559157.
- Плофкер, Ким (2001). «Ошибка» в индийском «приближении ряда Тейлора» к синусу ». Historia Mathematica. 28 (4): 283–295. Дои:10.1006 / hmat.2001.2331.
- Плокер, Ким (2007) "Математика в Индии". Математика Египта, Месопотамии, Китая, Индии и ислама: Справочник Нью-Джерси: Издательство Принстонского университета. ISBN 0-691-11485-4
- Пономарев, Леонид Иванович (1993). Квантовая игральная кость. CRC Press. ISBN 0-7503-0251-8.
- Поссель, Грегори Л. (2002). Цивилизация Инда: современная перспектива. Мэриленд: Роуман Альтамира. ISBN 0-7591-0172-8.
- Пратап, Ганган (март 2004 г.). «Индийская наука замедляется: упадок открытых исследований». Текущая наука. 86 (6): 768–769.
- Прути, Радж (2004). Предыстория и харапская цивилизация. Нью-Дели: APH Publishing Corp. ISBN 81-7648-581-0.
- Пурохит, Винаяк (1988). Искусство переходной Индии двадцатого века. Мумбаи: популярный Пракашан. ISBN 0-86132-138-3
- Путтасвами, Т. К. (2000), "Математические достижения древних индийских математиков". Математика в разных культурах: история незападной математики. Нью-Йорк: Издательство Springer. ISBN 0-7923-6481-3
- Рамакришнан, К. (октябрь 2001 г.). "In Memoriam: профессор Г. Н. Рамачандран (1922–2001)" (PDF). Белковая наука. 10 (8): 1689–1691. Дои:10.1002 / pro.101689. ЧВК 2374078. PMID 11468366. Получено 11 февраля 2009.
- Рао, С. (1985). Лотал. Археологические исследования Индии.
- Рао, К. Анантарама (2000). Видение 21 века. Индия: Издательство Vidya [Мичиган: Мичиганский университет]. ISBN 81-87699-00-0
- Прочтите, Питер Г. (2005) Геммология. Англия: Баттерворт-Хайнеманн. ISBN 0-7506-6449-5
- Рейнольдс, Терри S (1983). Сильнее сотни человек: история вертикального водяного колеса. Издательство Университета Джона Хопкинса. ISBN 0-8018-7248-0.
- Ригден, Джон С. (2005). Эйнштейн 1905: эталон величия. Массачусетс: Издательство Гарвардского университета. ISBN 0-674-01544-4.
- Робинсон, Динди и Эстес, Ребекка (1996). Мировые культуры через художественную деятельность. Нью-Гэмпшир: неограниченное количество библиотек. ISBN 1-56308-271-3.
- Родда и Убертини (2004). Основа цивилизации - наука о воде?. Международная ассоциация гидрологических наук. ISBN 1-901502-57-0.
- Русселе, Луи (1875). Индия и ее коренные принцы: путешествия по Центральной Индии и президентам Бомбея и Бенгалии. Лондон: Чепмен и Холл.
- Рой, Ранджан (1990), "Открытие формулы ряда для Лейбница, Грегори и Нилакантха ", Математический журнал (Математическая ассоциация Америки) 63 (5): 291–306
- Салиба, Джордж (1997). «Слияние азиатской и западной культур: исламская цивилизация и Европа до 1500 года». Азия в западной и мировой истории: руководство для преподавания. Отредактировано Эйнсли Томас Эмбри & Кэрол Глюк. Нью-Йорк: М.Э. Шарп. ISBN 1-56324-265-6.
- Санчес и Кантон (2006). Программирование микроконтроллера: Microchip PIC. CRC Press. ISBN 0-8493-7189-9.
- Саркар, Тапан К. и др. (2006), История беспроводной связи, Wiley-IEEE, ISBN 0-471-78301-3.
- Шафер, Эдвард Х. (1963). Золотые персики Самарканда: исследование танской экзотики. Калифорния: Калифорнийский университет Press. ISBN 0-520-05462-8.
- Шварцберг, Джозеф Э. (1992). «Часть 2: Картография Южной Азии: 15. Введение в картографию Южной Азии». История картографии - картография в традиционных исламских и южноазиатских обществах (Том 2 Книга 1). Отредактировано Дж. Б. Харли и Дэвид Вудворд. Нью-Йорк: Издательство Оксфордского университета США. ISBN 0-226-31635-1.
- Зайверт, Хуберт Майкл (2003). Популярные религиозные движения и гетеродоксальные секты в истории Китая. Массачусетс: Издательство Brill Academic Publishers. ISBN 90-04-13146-9.
- Шукла Р.П. в статье "Лазерные интерферометры для измерения показателя преломления прозрачных материалов и тестирования оптических компонентов", Применение лазеров в материаловедении и промышленности. 20–27. Союзные издатели. ISBN 81-7023-658-4.
- Сингх, А. Н. (1936). Об использовании рядов в индуистской математике. Осирис 1: 606–628.
- Сингх, Манпал (2005). Современное обучение математике. Дели: Anmol Publications Pvt Ltd. ISBN 81-261-2105-Х
- Сингх, П. (1985). Так называемые числа Фибоначчи в древней и средневековой Индии. Historia Mathematica 12 (3), 229–44.
- Sircar, округ Колумбия (1996).Индийская эпиграфика. Motilal Banarsidass. ISBN 81-208-1166-6.
- Сиварамакришнан, В. М. (2001). Табак и орех арека. Хайдарабад: Orient Blackswan. ISBN 81-250-2013-6
- Смит, Джозеф А. (1992). Книга "Перо и чернила": материалы и методы для современного художника. Нью-Йорк: публикации Watson-Guptill. ISBN 0-8230-3986-2.
- Смит, Дэвид Э. (1958). История математики. Courier Dover Publications. ISBN 0-486-20430-8.
- Срикантан, Б. В. (декабрь 2005 г.). «Хоми Бхабха и исследования космических лучей в Индии» (PDF). Резонанс. 10 (12): 42–51. Дои:10.1007 / BF02835127. S2CID 195305468.
- Шринивасан С. и Ранганатан С. Wootz Steel: передовой материал древнего мира. Бангалор: Индийский институт науки.
- Сринивасан, С. Тигельная сталь Wootz: недавно открытая производственная площадка в Южной Индии. Институт археологии, Университетский колледж Лондона, 5 (1994), стр. 49–61.
- Шринивасан С. и Гриффитс Д. Южно-индийский вуц: доказательства наличия высокоуглеродистой стали из тиглей из недавно обнаруженного участка и предварительные сравнения с соответствующими находками. Материальные проблемы в искусстве и археологии-V, Серия материалов симпозиума Общества исследования материалов, том. 462.
- Стаал, Фриц (1999). «Греческая и ведическая геометрия». Журнал индийской философии. 27 (1–2): 105–127. Дои:10.1023 / А: 1004364417713. S2CID 170894641.
- Щербацкий, Теодор (2003) [1930]. Буддийская логика. 1. Монтана: Kessinger Publishing. ISBN 978-0-7661-7684-3.
- Штейн, Бертон (1998). История Индии. Блэквелл Паблишинг. ISBN 0-631-20546-2.
- Степанов, Сергей А. (1999). Коды на алгебраических кривых. Springer. ISBN 0-306-46144-7.
- Стиллвелл, Джон (2004). Математика и ее история (2-е изд.). Берлин и Нью-Йорк: Springer. ISBN 0-387-95336-1.
- Тагучи, Геничи и Джугулум, Раджеш (2002). Стратегия Махаланобис-тагучи: система шаблонных технологий. Джон Уайли и сыновья. ISBN 0-471-02333-7.
- Терези, Дик; и другие. (2002). Утраченные открытия: древние корни современной науки - от вавилонян до майя. Нью-Йорк: Саймон и Шустер. ISBN 0-684-83718-8.
- Томас, Артур (2007) Драгоценные камни: свойства, идентификация и использование. Лондон: Издательство New Holland. ISBN 1-84537-602-1
- Трусфилд, Майкл (2007). Ветеринарная эпидемиология. Блэквелл Паблишинг. ISBN 1-4051-5627-9.
- Упадхьяя, Бхагват Саран (1954). Древний мир. Андхра-Прадеш: Институт древних исследований Хайдарабад.
- Варадпанде, Манохар Лаксман (2005). История индийского театра. Нью-Дели: публикации Abhinav. ISBN 81-7017-430-9.
- Венк, Ханс-Рудольф; и другие. (2003). Минералы: их состав и происхождение. Англия: Издательство Кембриджского университета. ISBN 0-521-52958-1.
- Whish, Чарльз (1835). «Об индуистской квадратуре круга и бесконечном ряду пропорций окружности к диаметру, показанных в четырех шастрах: Тантра Санграхам, Юкти-Бхаса, Чарана Падхати и Садратнамала». Сделки Королевского азиатского общества Великобритании и Ирландии. 3 (3): 509–523. Дои:10.1017 / S0950473700001221.
- Белый младший, Линн Таунсенд (1960). «Тибет, Индия и Малайя как источники западных средневековых технологий». Американский исторический обзор. 65 (3): 522–526. Дои:10.2307/1849619. JSTOR 1849619.
- Уайтлоу, Ян (2007). Мера всего: история человека и измерение. Macmillan. ISBN 0-312-37026-1.
- Уилкинсон, Чарльз К. (1943). «Шахматные фигуры и шахматы». Вестник Метрополитен-музея Новая серия. 1 (9): 271–279. Дои:10.2307/3257111. JSTOR 3257111.
- Мудрый, Тэд (2002). Благословения ветру: тайна и значение тибетских молитвенных флажков. Книги хроники. ISBN 0-8118-3435-2.
- Виссеман, С. У. и Уильямс, У. С. (1994). Древние технологии и археологические материалы. Лондон: Рутледж. ISBN 2-88124-632-X.
- Вудс, Майкл и Вудс, Мэри Б. (2000). Древний транспорт: от верблюдов до каналов. Миннесота: Книги двадцать первого века. ISBN 0-8225-2993-9.
внешняя ссылка
- Изобретения Древней Индии в области науки и техники
- Очерки индийской науки и техники.
- П. К. Рэй, НАУКА, КУЛЬТУРА И РАЗВИТИЕ - СВЯЗАННЫЕ ЯВЛЕНИЯ, Everyman's Science Vol.
- История науки в Южной Азии (hssa-journal.org ). HSSA - это рецензируемый онлайн-журнал с открытым доступом по истории науки в Индии.





