Теорема Нётерса - Википедия - Noethers theorem

Первая страница Эмми Нётер статья «Проблема инвариантных вариаций» (1918), в которой она доказала свою теорему.

Теорема Нётер или же Первая теорема Нётер заявляет, что каждый дифференцируемый симметрия из действие физической системы имеет соответствующий закон сохранения.^[1] Теорема была доказана математиком Эмми Нётер в 1915 г. и опубликовано в 1918 г.,^[2] после того, как особый случай был доказан Э. Коссера и Ф. Коссера в 1909 г.^[3] Действие физической системы - это интеграл с течением времени из Лагранжиан функция (которая может быть интеграл по пространству из Функция плотности лагранжиана ), из которого поведение системы может быть определено принцип наименьшего действия. Эта теорема применима только к непрерывным и гладким симметриям над физическое пространство.

Теорема Нётер используется в теоретическая физика и вариационное исчисление. Обобщение формулировок на постоянные движения в лагранжиане и Гамильтонова механика (разработан в 1788 и 1833 годах, соответственно), он не применяется к системам, которые нельзя моделировать одним лагранжианом (например, системы с Функция диссипации Рэлея ). Особенно, диссипативный системы с непрерывные симметрии не обязательно иметь соответствующий закон сохранения.

Основные иллюстрации и фон

Например, если физическая система ведет себя одинаково независимо от того, как она ориентирована в пространстве, ее Лагранжиан симметричен относительно непрерывных вращений: из этой симметрии теорема Нётер гласит, что угловой момент системы, как следствие ее законов движения. Сама физическая система не обязательно должна быть симметричной; зазубренный астероид, падающий в космосе, сохраняет угловой момент, несмотря на его асимметрию. Это законы его движения симметричны.

В качестве другого примера, если физический процесс демонстрирует одни и те же результаты независимо от места или времени, то его лагранжиан симметричен относительно непрерывных перемещений в пространстве и времени соответственно: по теореме Нётер эти симметрии объясняют законы сохранения из линейный импульс и энергия в рамках этой системы соответственно.

Теорема Нётер важна как из-за того, что она дает понимание законов сохранения, так и как практический инструмент для расчетов. Это позволяет исследователям определять сохраняющиеся величины (инварианты) из наблюдаемых симметрий физической системы. И наоборот, это позволяет исследователям рассматривать целые классы гипотетических лагранжианов с заданными инвариантами для описания физической системы. В качестве иллюстрации предположим, что предлагается физическая теория, сохраняющая величину Икс. Исследователь может вычислить типы лагранжианов, сохраняющих Икс через непрерывную симметрию. В соответствии с теоремой Нётер свойства этих лагранжианов предоставляют дополнительные критерии для понимания последствий и оценки пригодности новой теории.

Существует множество версий теоремы Нётер с разной степенью общности. У этой теоремы есть естественные квантовые аналоги, выраженные в Личности Уорда-Такахаши. Обобщения теоремы Нётер на суперпространства тоже существуют.^{[нужна цитата ]}

Неформальная формулировка теоремы

Помимо всех тонких технических моментов, теорему Нётер можно сформулировать неформально.

Если система обладает свойством непрерывной симметрии, то существуют соответствующие величины, значения которых сохраняются во времени.^[4]

Более сложная версия теоремы о полях утверждает, что:

Каждому дифференцируемому симметрия порожденный локальными действиями соответствует сохраненный ток.

Слово «симметрия» в приведенном выше утверждении более точно относится к ковариация формы, которую принимает физический закон по отношению к одномерному Группа Ли преобразований, удовлетворяющих определенным техническим критериям. В закон сохранения из физическое количество обычно выражается как уравнение неразрывности.

Формальное доказательство теоремы использует условие инвариантности, чтобы получить выражение для тока, связанного с сохраняющейся физической величиной. В современном (с 1980 г.^[5]) по терминологии сохраняющаяся величина называется Нётер заряд, а поток, несущий этот заряд, называется Ток Нётер. Ток Нётер определяется вплоть до а соленоидный (бездивергентное) векторное поле.

В контексте гравитации Феликс Кляйн Утверждение теоремы Нётер о действии я предусматривает для инвариантов:^[6]

Если интеграл I инвариантен относительно непрерывной группы грамм_ρ с ρ параметры, то ρ линейно независимые комбинации лагранжевых выражений являются расходимостями.

Краткая иллюстрация и обзор концепции

График, иллюстрирующий теорему Нётер для покоординатной симметрии.

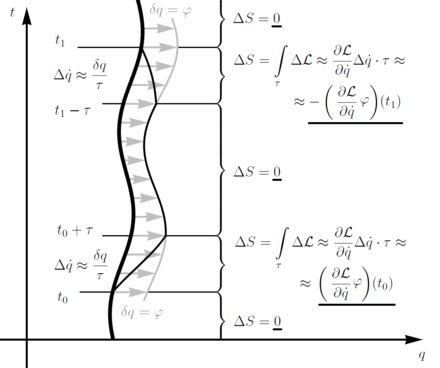
Основная идея теоремы Нётер легче всего иллюстрируется системой с одной координатой ${ displaystyle q}$ и непрерывная симметрия ${ displaystyle varphi: q mapsto q + delta q}$ (серые стрелки на схеме). Рассмотрим любую траекторию ${ displaystyle q (t)}$ (жирный на схеме), удовлетворяющий законы движения. Это действие ${ displaystyle S}$ управление этой системой стационарный на этой траектории, т.е. не меняется ни при каких локальных вариация траектории. В частности, он не изменится при вариации, в которой применяется поток симметрии ${ displaystyle varphi}$ на временном отрезке [т₀, т₁] и неподвижен вне этого сегмента. Чтобы траектория оставалась непрерывной, мы используем периоды "буферизации" небольшого времени. ${ Displaystyle тау}$ переходить между сегментами постепенно.

Полное изменение действия ${ displaystyle S}$ теперь включает изменения, вносимые каждым интервалом в игре. Части, в которых исчезает сама вариация, не приносят ${ displaystyle Delta S}$. Средняя часть тоже не меняет действия, потому что ее трансформация ${ displaystyle varphi}$ является симметрией и, таким образом, сохраняет лагранжиан ${ displaystyle L}$ и действие ${ textstyle S = int L}$. Единственные оставшиеся части - это «буферные» части. Грубо говоря, они вносят свой вклад в основном своей "косой" ${ displaystyle { dot {q}} rightarrow { dot {q}} pm delta q / tau}$.

Это изменяет лагранжиан на ${ Displaystyle Delta L приблизительно { bigl (} partial L / partial { dot {q}} { bigr)} Delta { dot {q}}}$, который интегрируется в

${ displaystyle Delta S = int Delta L приблизительно int { frac { partial L} { partial { dot {q}}}} Delta { dot {q}} приблизительно int { frac { partial L} { partial { dot {q}}}} { Bigl (} pm { frac { delta q} { tau}} { Bigr)} приблизительно pm { frac { partial L} { partial { dot {q}}}} delta q = pm { frac { partial L} { partial { dot {q}}}} varphi}$.

Эти последние термины, оцениваемые по конечным точкам ${ displaystyle t_ {0}}$ и ${ displaystyle t_ {1}}$, должны отменять друг друга, чтобы полностью изменить действие ${ displaystyle Delta S}$ равняется нулю, как и следовало ожидать, если траектория является решением. То есть

${ Displaystyle { Bigl (} { frac { partial L} { partial { dot {q}}}} varphi { Bigr)} (t_ {0}) = { Bigl (} { frac { partial L} { partial { dot {q}}}} varphi { Bigr)} (t_ {1})}$,

имея в виду количество ${ Displaystyle { bigl (} partial L / partial { dot {q}} { bigr)} varphi}$ сохраняется, что является заключением теоремы Нётер. Например, если чистые переводы ${ displaystyle varphi = const }$ симметрия, то сохраняющаяся величина становится просто ${ Displaystyle { bigl (} partial L / partial { dot {q}} { bigr)} = p}$, канонический импульс.

Более общие случаи следуют той же идее:

Когда больше координат ${ displaystyle q_ {r}}$ претерпеть преобразование симметрии ${ displaystyle q_ {r} mapsto q_ {r} + varphi _ {r}}$, их эффекты складываются по линейности в сохраняющуюся величину ${ displaystyle sum _ {r} { bigl (} partial L / partial { dot {q}} _ {r} { bigr)} varphi _ {r}}$.

Когда есть временные трансформации ${ Displaystyle т mapsto т + Т}$, они заставляют сегменты "буферизации" вносить два следующих члена в ${ displaystyle Delta S}$:

${ displaystyle Delta S приблизительно pm { Bigl (} TL + int { frac { partial L} { partial { dot {q}} _ {r}}} Delta { dot {q} } _ {r} { Bigr)} приблизительно pm T { Bigl (} L - { frac { partial L} { partial { dot {q}} _ {r}}} { dot { q}} _ {r} { Bigr)}}$,

первый член обусловлен растяжением во временном измерении сегмента «буферизации» (который изменяет размер области интеграции), а второй - его «наклоном», как в примерном случае. Вместе они добавляют слагаемое ${ displaystyle T { Bigl (} L- sum _ {r} { bigl (} partial L / partial { dot {q}} _ {r} { bigr)} { dot {q} } _ {r} { Bigr)}}$ к сохраненному количеству.

Наконец, когда вместо траектории ${ displaystyle q (t)}$ целые поля ${ displaystyle psi (q_ {r}, t)}$ рассматриваются, аргумент заменяет

• интервал ${ Displaystyle [т_ {0}, т_ {1}]}$ с ограниченной областью ${ displaystyle U}$ из ${ displaystyle (q_ {r}, t)}$-домен,
• конечные точки ${ displaystyle t_ {0}}$ и ${ displaystyle t_ {1}}$ с границей ${ displaystyle partial U}$ области,
• и его вклад в ${ displaystyle Delta S}$ интерпретируется как поток сохраненный ток ${ displaystyle j_ {r}}$, который построен аналогично предыдущему определению сохраняемой величины.

Теперь нулевой вклад "буферизации" ${ displaystyle partial U}$ к ${ displaystyle Delta S}$ интерпретируется как обращение в нуль полного потока тока ${ displaystyle j_ {r}}$ сквозь ${ displaystyle partial U}$. В этом смысле он сохраняется: сколько «втекает», столько же «вытекает».

Исторический контекст

А закон сохранения заявляет, что некоторое количество Икс в математическом описании эволюции системы остается неизменным на протяжении всего ее движения - это инвариантный. Математически скорость изменения Икс (это производная относительно время ) равен нулю,

${ displaystyle { frac {dX} {dt}} = { dot {X}} = 0 ~.}$

Говорят, что такие количества сохраняются; их часто называют постоянные движения (хотя движение как таковой не нужно участвовать, просто эволюция во времени). Например, если энергия системы сохраняется, ее энергия всегда инвариантна, что накладывает ограничение на движение системы и может помочь в ее решении. Помимо понимания природы системы, которое такие постоянные движения дают, они являются полезным инструментом расчетов; например, приближенное решение можно исправить, найдя ближайшее состояние, удовлетворяющее подходящим законам сохранения.

Самые ранние обнаруженные константы движения были импульс и энергия, которые были предложены в 17 веке Рене Декарт и Готфрид Лейбниц на основе столкновение экспериментов и уточнены последующими исследователями. Исаак Ньютон был первым, кто провозгласил сохранение импульса в его современной форме, и показал, что это является следствием Третий закон Ньютона. В соответствии с общая теория относительности, законы сохранения количества движения, энергии и момента количества движения в целом справедливы только тогда, когда они выражаются через сумму тензор энергии-импульса (негравитационное напряжение – энергия) и Псевдотензор напряжения – энергии – импульса Ландау – Лифшица (гравитационное напряжение – энергия). Локальное сохранение негравитационного импульса и энергии в свободно падающей системе отсчета выражается обращением в нуль ковариантной расхождение из тензор энергии-импульса. Еще одна важная сохраняющаяся величина, обнаруженная в исследованиях небесная механика астрономических тел, это Вектор Лапласа – Рунге – Ленца..

В конце 18 - начале 19 вв. Физики разработали более систематические методы открытия инвариантов. Главный прорыв произошел в 1788 году с развитием Лагранжева механика, что связано с принцип наименьшего действия. При таком подходе состояние системы может быть описано любым типом обобщенные координаты q; законы движения не обязательно выражать в Декартова система координат, как это было принято в механике Ньютона. В действие определяется как интеграл по времени я функции, известной как Лагранжиан  L

${ Displaystyle I = int L ( mathbf {q}, { dot { mathbf {q}}}, t) , dt ~,}$

где точка над q означает скорость изменения координат q,

${ displaystyle { dot { mathbf {q}}} = { frac {d mathbf {q}} {dt}} ~.}$

Принцип Гамильтона утверждает, что физический путь q(т) - фактически пройденный системой - путь, для которого бесконечно малые вариации этого пути не вызывают изменения в я, по крайней мере, до первого порядка. Этот принцип приводит к Уравнения Эйлера – Лагранжа.,

${ displaystyle { frac {d} {dt}} left ({ frac { partial L} { partial { dot { mathbf {q}}}}} right) = { frac { partial L} { partial mathbf {q}}} ~.}$

Таким образом, если одна из координат, скажем, q_k, не входит в лагранжиан, правая часть уравнения равна нулю, а левая часть требует, чтобы

${ displaystyle { frac {d} {dt}} left ({ frac { partial L} { partial { dot {q}} _ {k}}} right) = { frac {dp_ { k}} {dt}} = 0 ~,}$

где импульс

${ displaystyle p_ {k} = { frac { partial L} { partial { dot {q}} _ {k}}}}$

сохраняется на протяжении всего движения (на физическом пути).

Таким образом, отсутствие игнорируемый координировать q_k из лагранжиана означает, что на лагранжиан не влияют изменения или преобразования q_k; лагранжиан инвариантен и, как говорят, обладает симметрия при таких преобразованиях. Это основная идея, обобщенная в теореме Нётер.

Несколько альтернативных методов поиска сохраняемых количеств были разработаны в 19 веке, особенно Уильям Роуэн Гамильтон. Например, он разработал теорию канонические преобразования что позволило изменить координаты так, чтобы некоторые координаты исчезли из лагранжиана, как указано выше, что привело к сохранению канонических импульсов. Другой подход и, возможно, наиболее эффективный для поиска сохраняющихся величин, - это Уравнение Гамильтона – Якоби.

Математическое выражение

Простая форма с использованием возмущений

Суть теоремы Нётер сводится к обобщению изложенных игнорируемых координат.^{[требуется разъяснение ]}

Можно считать, что лагранжиан L определенная выше, инвариантна относительно малых возмущений (деформаций) временной переменной т и обобщенные координаты q. Можно написать

${ displaystyle t rightarrow t ^ { prime} = t + delta t}$

${ displaystyle mathbf {q} rightarrow mathbf {q} ^ { prime} = mathbf {q} + delta mathbf {q} ~,}$

где возмущения δt и δq оба маленькие, но изменчивые. Для общности предположим, что есть (скажем) N такой преобразования симметрии действия, т. е. преобразований, оставляющих действие неизменным; помечены индексом р = 1, 2, 3, ..., N.

Тогда возникающее возмущение можно записать как линейную сумму отдельных типов возмущений:

${ displaystyle delta t = sum _ {r} varepsilon _ {r} T_ {r}}$

${ displaystyle delta mathbf {q} = sum _ {r} varepsilon _ {r} mathbf {Q} _ {r} ~,}$

куда ε_р находятся бесконечно малый коэффициенты параметров, соответствующие каждому:

• генератор Т_р из эволюция во времени, и
• генератор Q_р обобщенных координат.

Для переводов, Q_р постоянная с единицами измерения длина; для вращений это выражение, линейное по компонентам q, а параметры составляют угол.

Используя эти определения, Нётер показал, что N количество

${ displaystyle left ({ frac { partial L} { partial { dot { mathbf {q}}}}} cdot { dot { mathbf {q}}} - L right) T_ { r} - { frac { partial L} { partial { dot { mathbf {q}}}}} cdot mathbf {Q} _ {r}}$

(которые имеют размеры [энергия] · [время] + [импульс] · [длина] = [действие]) сохраняются (постоянные движения ).

Примеры

Инвариантность во времени

Для иллюстрации рассмотрим лагранжиан, не зависящий от времени, т.е. инвариантный (симметричный) относительно изменений т → т + δт, без изменения координат q. В этом случае, N = 1, Т = 1 и Q = 0; соответствующая сохраняющаяся величина - это полная энергия ЧАС^[7]

${ displaystyle H = { frac { partial L} { partial { dot { mathbf {q}}}}} cdot { dot { mathbf {q}}} - L.}$

Трансляционная инвариантность

Рассмотрим лагранжиан, который не зависит от координаты («игнорируемой», как указано выше) q_k; поэтому он инвариантен (симметричен) относительно изменений q_k → q_k + δq_k. В таком случае, N = 1, Т = 0 и Q_k = 1; сохраняющаяся величина - соответствующая линейная импульс п_k^[8]

${ displaystyle p_ {k} = { frac { partial L} { partial { dot {q_ {k}}}}}.}$

В специальный и общая теория относительности эти явно отдельные законы сохранения являются аспектами единого закона сохранения тензор энергии-импульса,^[9] это выводится в следующем разделе.

Вращательная инвариантность

Сохранение угловой момент L = р × п аналогичен своему аналогу по линейному импульсу.^[10] Предполагается, что симметрия лагранжиана вращательная, т.е. что лагранжиан не зависит от абсолютной ориентации физической системы в пространстве. Для конкретности предположим, что лагранжиан не меняется при малых поворотах на угол δθ вокруг оси п; такое вращение преобразует Декартовы координаты по уравнению

${ displaystyle mathbf {r} rightarrow mathbf {r} + delta theta , mathbf {n} times mathbf {r}.}$

Поскольку время не преображается, Т= 0. Принимая δθ как ε параметр и декартовы координаты р как обобщенные координаты qсоответствующие Q переменные задаются

${ displaystyle mathbf {Q} = mathbf {n} times mathbf {r}.}$

Тогда теорема Нётер утверждает, что сохраняется следующая величина:

${ displaystyle { frac { partial L} { partial { dot { mathbf {q}}}}} cdot mathbf {Q} _ {r} = mathbf {p} cdot left ( mathbf {n} times mathbf {r} right) = mathbf {n} cdot left ( mathbf {r} times mathbf {p} right) = mathbf {n} cdot mathbf {L}.}$

Другими словами, составляющая момента количества движения L вдоль п ось сохраняется.

Если п произвольно, т.е. если система нечувствительна к какому-либо вращению, то каждая компонента L сохраняется; короче, угловой момент сохраняется.

Версия теории поля

Приведенная версия теоремы Нётер полезна сама по себе, но она является частным случаем общей версии, полученной в 1915 году. Чтобы придать изюминку общей теоремы, версия теоремы Нётер для непрерывных полей в четырехмерном пространстве. пространство-время теперь дано. Поскольку задачи теории поля более распространены в современной физике, чем механика проблем, эта версия теории поля является наиболее часто используемой (или наиболее часто применяемой) версией теоремы Нётер.

Пусть существует набор дифференцируемых поля ${ displaystyle varphi}$ определяется во всем пространстве и времени; например, температура ${ Displaystyle Т ( mathbf {х}, т)}$ будет представлять такое поле, будучи числом, определяемым в каждом месте и в любое время. В принцип наименьшего действия могут быть применены к таким полям, но теперь действие является интегралом по пространству и времени

${ Displaystyle { mathcal {S}} = int { mathcal {L}} left ( varphi, partial _ { mu} varphi, x ^ { mu} right) , d ^ { 4} x}$

(теорему можно далее обобщить на случай, когда лагранжиан зависит от п^th производная, а также может быть сформулирована с использованием жгуты ).

Непрерывное преобразование полей ${ displaystyle varphi}$ можно записать бесконечно малым образом как

${ Displaystyle varphi mapsto varphi + varepsilon Psi,}$

куда ${ displaystyle Psi}$ в общем, функция, которая может зависеть от обоих ${ displaystyle x ^ { mu}}$ и ${ displaystyle varphi}$. Условие для ${ displaystyle Psi}$ для создания физической симметрии действие ${ Displaystyle { mathcal {S}}}$ остается инвариантным. Это, безусловно, будет верно, если плотность лагранжиана ${ Displaystyle { mathcal {L}}}$ остается инвариантным, но оно также будет истинным, если лагранжиан изменится на расхождение,

${ Displaystyle { mathcal {L}} mapsto { mathcal {L}} + varepsilon partial _ { mu} Lambda ^ { mu},}$

так как интеграл от расходимости становится граничным членом согласно теорема расходимости. Система, описываемая данным действием, может иметь несколько независимых симметрий этого типа, индексированных ${ Displaystyle г = 1,2, ldots, N,}$ так что наиболее общее преобразование симметрии будет записано как

${ Displaystyle varphi mapsto varphi + varepsilon _ {r} Psi _ {r},}$

со следствием

${ displaystyle { mathcal {L}} mapsto { mathcal {L}} + varepsilon _ {r} partial _ { mu} Lambda _ {r} ^ { mu}.}$

Для таких систем теорема Нётер утверждает, что существуют ${ displaystyle N}$ консервированный текущие плотности

${ displaystyle j_ {r} ^ { nu} = Lambda _ {r} ^ { nu} - { frac { partial { mathcal {L}}} { partial varphi _ {, nu} }} cdot Psi _ {r}}$

(где скалярное произведение сокращает поле индексы, а не ${ displaystyle nu}$ index или ${ displaystyle r}$ индекс).

В таких случаях закон сохранения выражается в четырехмерном виде

${ displaystyle partial _ { nu} j ^ { nu} = 0,}$

который выражает идею о том, что количество сохраняющейся величины внутри сферы не может измениться, если некоторая часть не вытекает из сферы. Например, электрический заряд сохраняется; количество заряда внутри сферы не может измениться, если часть заряда не покинет сферу.

Для иллюстрации рассмотрим физическую систему полей, которая ведет себя одинаково при перемещениях во времени и пространстве, как рассмотрено выше; другими словами, ${ displaystyle L left ({ boldsymbol { varphi}}, partial _ { mu} { boldsymbol { varphi}}, x ^ { mu} right)}$ постоянна в своем третьем аргументе. В таком случае, N = 4, по одному для каждого измерения пространства и времени. Бесконечно малый перенос в пространстве, ${ displaystyle x ^ { mu} mapsto x ^ { mu} + varepsilon _ {r} delta _ {r} ^ { mu}}$ (с ${ displaystyle delta}$ обозначая Дельта Кронекера ), влияет на поля как ${ displaystyle varphi (x ^ { mu}) mapsto varphi (x ^ { mu} - varepsilon _ {r} delta _ {r} ^ { mu})}$: то есть изменение метки координат эквивалентно оставлению координат на месте при переводе самого поля, что, в свою очередь, эквивалентно преобразованию поля путем замены его значения в каждой точке ${ displaystyle x ^ { mu}}$ со значением в точке ${ displaystyle x ^ { mu} - varepsilon X ^ { mu}}$ "позади", который будет отображен на ${ displaystyle x ^ { mu}}$ рассматриваемым бесконечно малым смещением. Поскольку это бесконечно мало, мы можем записать это преобразование как

${ displaystyle Psi _ {r} = - delta _ {r} ^ { mu} partial _ { mu} varphi.}$

Таким же образом преобразуется плотность лагранжиана: ${ displaystyle { mathcal {L}} (x ^ { mu}) mapsto { mathcal {L}} (x ^ { mu} - varepsilon _ {r} delta _ {r} ^ { mu})}$, так

${ displaystyle Lambda _ {r} ^ { mu} = - delta _ {r} ^ { mu} { mathcal {L}}}$

и, таким образом, теорема Нётер соответствует закону сохранения тензор энергии-импульса Т_μ^ν,^[9] где мы использовали ${ displaystyle mu}$ на месте ${ displaystyle r}$. То есть, используя выражение, данное ранее, и собирая четыре сохраняющихся тока (по одному для каждого ${ displaystyle mu}$) в тензор ${ displaystyle T}$, Теорема Нётер дает

${ displaystyle T _ { mu} {} ^ { nu} = - delta _ { mu} ^ { nu} { mathcal {L}} + delta _ { mu} ^ { sigma} partial _ { sigma} varphi { frac { partial { mathcal {L}}} { partial varphi _ {, nu}}} = left ({ frac { partial { mathcal {L }}} { partial varphi _ {, nu}}} right) cdot varphi _ {, mu} - delta _ { mu} ^ { nu} { mathcal {L}}}$

с

${ displaystyle T _ { mu} {} ^ { nu} {} _ {, nu} = 0}$

(мы переименовали ${ displaystyle mu}$ в качестве ${ displaystyle sigma}$ на промежуточном этапе, чтобы избежать конфликта). (Тем не менее ${ displaystyle T}$ полученный таким образом может отличаться от симметричного тензора, используемого в качестве источника в общей теории относительности; видеть Канонический тензор энергии-импульса.)

Сохранение электрический заряд, напротив, можно получить, рассматривая Ψ линейный по полям φ а не в производных.^[11] В квантовая механика, то амплитуда вероятности ψ(Икс) нахождения частицы в точке Икс это сложное поле φ, потому что он приписывает комплексное число в каждую точку пространства и времени. Сама амплитуда вероятности физически неизмерима; только вероятность п = |ψ|² можно сделать вывод из набора измерений. Следовательно, система инвариантна относительно преобразований ψ поле и его комплексно сопряженный поле ψ^* что оставить |ψ|² без изменений, например

${ displaystyle psi rightarrow e ^ {я theta} psi , psi ^ {*} rightarrow e ^ {- i theta} psi ^ {*} ~,}$

сложное вращение. В пределе, когда фаза θ становится бесконечно малым, δθ, его можно принять как параметр ε, в то время как Ψ равны iψ и -iψ*, соответственно. Конкретным примером является Уравнение Клейна – Гордона, то релятивистски правильный версия Уравнение Шредингера за бесспиновый частиц, имеющего лагранжиан плотность

${ Displaystyle L = psi _ {, nu} psi _ {, mu} ^ {*} eta ^ { nu mu} + m ^ {2} psi psi ^ {*}.}$

В этом случае теорема Нётер утверждает, что сохраняющееся (∂ ⋅j = 0) ток равен

${ Displaystyle j ^ { nu} = я влево ({ frac { partial psi} { partial x ^ { mu}}} psi ^ {*} - { frac { partial psi ^ {*}} { partial x ^ { mu}}} psi right) eta ^ { nu mu} ~,}$

который, умноженный на заряд частицы этого типа, равен плотности электрического тока, обусловленной этим типом частицы. Эта «калибровочная инвариантность» впервые была отмечена Герман Вейль, и является одним из прототипов калибровочные симметрии физики.

Производные

Одна независимая переменная

Рассмотрим простейший случай - систему с одной независимой переменной - временем. Предположим, что зависимые переменные q таковы, что интеграл действия

${ Displaystyle I = int _ {t_ {1}} ^ {t_ {2}} L [ mathbf {q} [t], { dot { mathbf {q}}} [t], t] , dt}$

инвариантен относительно кратких бесконечно малых изменений зависимых переменных. Другими словами, они удовлетворяют Уравнения Эйлера – Лагранжа.

${ displaystyle { frac {d} {dt}} { frac { partial L} { partial { dot { mathbf {q}}}}} [t] = { frac { partial L} { partial mathbf {q}}} [t].}$

И предположим, что интеграл инвариантен относительно непрерывной симметрии. Математически такая симметрия представлена ​​как поток, φ, который действует на переменные следующим образом

${ displaystyle t rightarrow t '= t + varepsilon T}$

${ displaystyle mathbf {q} [t] rightarrow mathbf {q} '[t'] = varphi [ mathbf {q} [t], varepsilon] = varphi [ mathbf {q} [t '- varepsilon T], varepsilon]}$

куда ε - реальная переменная, указывающая количество потока, и Т - реальная константа (которая может быть равна нулю), показывающая, насколько поток сдвигает время.

${ displaystyle { dot { mathbf {q}}} [t] rightarrow { dot { mathbf {q}}} '[t'] = { frac {d} {dt}} varphi [ mathbf {q} [t], varepsilon] = { frac { partial varphi} { partial mathbf {q}}} [ mathbf {q} [t '- varepsilon T], varepsilon] { dot { mathbf {q}}} [t '- varepsilon T].}$

Интеграл действия течет к

${ displaystyle { begin {align} I '[ varepsilon] & = int _ {t_ {1} + varepsilon T} ^ {t_ {2} + varepsilon T} L [ mathbf {q}' [ t '], { dot { mathbf {q}}}' [t '], t'] , dt ' [6pt] & = int _ {t_ {1} + varepsilon T} ^ { t_ {2} + varepsilon T} L [ varphi [ mathbf {q} [t '- varepsilon T], varepsilon], { frac { partial varphi} { partial mathbf {q}} } [ mathbf {q} [t '- varepsilon T], varepsilon] { dot { mathbf {q}}} [t' - varepsilon T], t '] , dt' end {выровнено }}}$

что можно рассматривать как функцию ε. Вычисление производной при ε ' = 0 и используя Правило Лейбница, мы получили

${ displaystyle { begin {align} 0 = {} & { frac {dI '} {d varepsilon}} [0] = L [ mathbf {q} [t_ {2}], { dot { mathbf {q}}} [t_ {2}], t_ {2}] TL [ mathbf {q} [t_ {1}], { dot { mathbf {q}}} [t_ {1}], t_ {1}] T [6pt] & {} + int _ {t_ {1}} ^ {t_ {2}} { frac { partial L} { partial mathbf {q}}} left (- { frac { partial varphi} { partial mathbf {q}}} { dot { mathbf {q}}} T + { frac { partial varphi} { partial varepsilon}} right) + { frac { partial L} { partial { dot { mathbf {q}}}}} left (- { frac { partial ^ {2} varphi} {( partial mathbf {q}) ^ {2}}} { dot { mathbf {q}}} ^ {2} T + { frac { partial ^ {2} varphi} { partial varepsilon partial mathbf { q}}} { dot { mathbf {q}}} - { frac { partial varphi} { partial mathbf {q}}} { ddot { mathbf {q}}} T right) , дт. конец {выровнено}}}$

Обратите внимание, что из уравнений Эйлера – Лагранжа следует

${ displaystyle { begin {align} { frac {d} {dt}} left ({ frac { partial L} { partial { dot { mathbf {q}}}}}} { frac { partial varphi} { partial mathbf {q}}} { dot { mathbf {q}}} T right) & = left ({ frac {d} {dt}} { frac { частичное L} { partial { dot { mathbf {q}}}} right) { frac { partial varphi} { partial mathbf {q}}} { dot { mathbf {q} }} T + { frac { partial L} { partial { dot { mathbf {q}}}}} left ({ frac {d} {dt}} { frac { partial varphi} { partial mathbf {q}}} right) { dot { mathbf {q}}} T + { frac { partial L} { partial { dot { mathbf {q}}}}} { frac { partial varphi} { partial mathbf {q}}} { ddot { mathbf {q}}} , T [6pt] & = { frac { partial L} { partial mathbf {q}}} { frac { partial varphi} { partial mathbf {q}}} { dot { mathbf {q}}} T + { frac { partial L} { partial { точка { mathbf {q}}}}} left ({ frac { partial ^ {2} varphi} {( partial mathbf {q}) ^ {2}}} { dot { mathbf { q}}} right) { dot { mathbf {q}}} T + { frac { partial L} { partial { dot { mathbf {q}}}}} { frac { partial varphi} { partial mathbf {q}}} { ddot { mathbf {q}}} , T. end {align}}}$

Подставляя это в предыдущее уравнение, получаем

${ displaystyle { begin {align} 0 = {} & { frac {dI '} {d varepsilon}} [0] [6pt] = {} & L [ mathbf {q} [t_ {2} ], { dot { mathbf {q}}} [t_ {2}], t_ {2}] TL [ mathbf {q} [t_ {1}], { dot { mathbf {q}}} [t_ {1}], t_ {1}] T - { frac { partial L} { partial { dot { mathbf {q}}}}} { frac { partial varphi} { partial mathbf {q}}} { dot { mathbf {q}}} [t_ {2}] T + { frac { partial L} { partial { dot { mathbf {q}}}}} { frac { partial varphi} { partial mathbf {q}}} { dot { mathbf {q}}} [t_ {1}] T [6pt] & {} + int _ {t_ {1}} ^ {t_ {2}} { frac { partial L} { partial mathbf {q}}} { frac { partial varphi} { partial varepsilon}} + { frac { partial L} { partial { dot { mathbf {q}}}}} { frac { partial ^ {2} varphi} { partial varepsilon partial mathbf {q}}} { dot { mathbf {q}}} , дт. конец {выровнено}}}$

Снова используя уравнения Эйлера – Лагранжа, получаем

${ displaystyle { frac {d} {dt}} left ({ frac { partial L} { partial { dot { mathbf {q}}}}}} { frac { partial varphi} { partial varepsilon}} right) = left ({ frac {d} {dt}} { frac { partial L} { partial { dot { mathbf {q}}}}} right) { frac { partial varphi} { partial varepsilon}} + { frac { partial L} { partial { dot { mathbf {q}}}}} { frac { partial ^ {2 } varphi} { partial varepsilon partial mathbf {q}}} { dot { mathbf {q}}} = { frac { partial L} { partial mathbf {q}}} { frac { partial varphi} { partial varepsilon}} + { frac { partial L} { partial { dot { mathbf {q}}}}} { frac { partial ^ {2} varphi} { partial varepsilon partial mathbf {q}}} { dot { mathbf {q}}}.}$

Подставляя это в предыдущее уравнение, получаем

${ displaystyle { begin {align} 0 = {} & L [ mathbf {q} [t_ {2}], { dot { mathbf {q}}} [t_ {2}], t_ {2}] TL [ mathbf {q} [t_ {1}], { dot { mathbf {q}}} [t_ {1}], t_ {1}] T - { frac { partial L} { partial { dot { mathbf {q}}}}} { frac { partial varphi} { partial mathbf {q}}} { dot { mathbf {q}}} [t_ {2}] T + { frac { partial L} { partial { dot { mathbf {q}}}}} { frac { partial varphi} { partial mathbf {q}}} { dot { mathbf { q}}} [t_ {1}] T [6pt] & {} + { frac { partial L} { partial { dot { mathbf {q}}}}} { frac { partial varphi} { partial varepsilon}} [t_ {2}] - { frac { partial L} { partial { dot { mathbf {q}}}}} { frac { partial varphi} { partial varepsilon}} [t_ {1}]. end {align}}}$

Из чего видно, что

${ displaystyle left ({ frac { partial L} { partial { dot { mathbf {q}}}}} { frac { partial varphi} { partial mathbf {q}}} { dot { mathbf {q}}} - L right) T - { frac { partial L} { partial { dot { mathbf {q}}}}} { frac { partial varphi} { partial varepsilon}}}$

постоянная движения, т. е. сохраняющаяся величина. Поскольку φ [q, 0] = q, мы получили ${ displaystyle { frac { partial varphi} { partial mathbf {q}}} = 1}$ и поэтому сохраняемая величина упрощается до

${ displaystyle left ({ frac { partial L} { partial { dot { mathbf {q}}}}} { dot { mathbf {q}}} - L right) T - { frac { partial L} { partial { dot { mathbf {q}}}}} { frac { partial varphi} { partial varepsilon}}.}$

Чтобы избежать чрезмерного усложнения формул, в этом выводе предполагается, что поток не меняется с течением времени. Тот же результат можно получить и в более общем случае.

Теоретико-полевой вывод

Теорема Нётер также может быть получена для тензорных полей. φ^А где индекс А пробегает различные компоненты различных тензорных полей. Эти величины поля представляют собой функции, определенные в четырехмерном пространстве, точки которого помечены координатами Икс^μ где индекс μ колеблется во времени (μ = 0) и трех пространственных измерений (μ = 1, 2, 3). Эти четыре координаты являются независимыми переменными; и значения полей в каждом событии являются зависимыми переменными. При бесконечно малом преобразовании изменение координат записывается как

${ displaystyle x ^ { mu} rightarrow xi ^ { mu} = x ^ { mu} + delta x ^ { mu}}$

тогда как преобразование переменных поля выражается как

${ Displaystyle varphi ^ {A} rightarrow alpha ^ {A} ( xi ^ { mu}) = varphi ^ {A} (x ^ { mu}) + delta varphi ^ {A} (х ^ { mu}) ,.}$

По этому определению вариации поля δφ^А являются результатом двух факторов: внутренних изменений самого поля и изменений координат, поскольку преобразованное поле α^А зависит от преобразованных координат ξ^μ. Чтобы изолировать внутренние изменения, вариация поля в одной точке Икс^μ можно определить

${ displaystyle alpha ^ {A} (x ^ { mu}) = varphi ^ {A} (x ^ { mu}) + { bar { delta}} varphi ^ {A} (x ^ { mu}) ,.}$

Если координаты меняются, граница области пространства-времени, по которой интегрируется лагранжиан, также изменяется; исходная граница и ее преобразованная версия обозначаются как Ω и Ω ’соответственно.

Теорема Нётер начинается с предположения, что конкретное преобразование координат и переменных поля не меняет действие, который определяется как интеграл плотности лагранжиана по заданной области пространства-времени. Математически это предположение может быть записано как

${ displaystyle int _ { Omega ^ { prime}} L left ( alpha ^ {A}, { alpha ^ {A}} _ {, nu}, xi ^ { mu} right ) d ^ {4} xi - int _ { Omega} L left ( varphi ^ {A}, { varphi ^ {A}} _ {, nu}, x ^ { mu} right ) d ^ {4} x = 0}$

где нижний индекс запятой указывает частную производную по координате (ях), которая следует за запятой, например

${ displaystyle { varphi ^ {A}} _ {, sigma} = { frac { partial varphi ^ {A}} { partial x ^ { sigma}}} ,.}$

Поскольку ξ - фиктивная переменная интегрирования, и поскольку изменение границы Ω бесконечно мало по предположению, два интеграла могут быть объединены с использованием четырехмерной версии теорема расходимости в следующую форму

${ Displaystyle int _ { Omega} left { left [L left ( alpha ^ {A}, { alpha ^ {A}} _ {, nu}, x ^ { mu} right) -L left ( varphi ^ {A}, { varphi ^ {A}} _ {, nu}, x ^ { mu} right) right] + { frac { partial} { partial x ^ { sigma}}} left [L left ( varphi ^ {A}, { varphi ^ {A}} _ {, nu}, x ^ { mu} right) delta x ^ { sigma} right] right } d ^ {4} x = 0 ,.}$

Разность лагранжианов может быть записана в первом порядке по бесконечно малым вариациям как

${ displaystyle left [L left ( alpha ^ {A}, { alpha ^ {A}} _ {, nu}, x ^ { mu} right) -L left ( varphi ^ { A}, { varphi ^ {A}} _ {, nu}, x ^ { mu} right) right] = { frac { partial L} { partial varphi ^ {A}}} { bar { delta}} varphi ^ {A} + { frac { partial L} { partial { varphi ^ {A}} _ {, sigma}}} { bar { delta}} { varphi ^ {A}} _ {, sigma} ,.}$

Однако, поскольку вариации определяются в той же точке, что и описано выше, вариация и производная могут быть выполнены в обратном порядке; Oни ездить

${ displaystyle { bar { delta}} { varphi ^ {A}} _ {, sigma} = { bar { delta}} { frac { partial varphi ^ {A}} { partial x ^ { sigma}}} = { frac { partial} { partial x ^ { sigma}}} ({ bar { delta}} varphi ^ {A}) ,.}$

Используя уравнения поля Эйлера – Лагранжа

${ displaystyle { frac { partial} { partial x ^ { sigma}}} left ({ frac { partial L} { partial { varphi ^ {A}} _ {, sigma}} } right) = { frac { partial L} { partial varphi ^ {A}}}}$

разницу в лагранжианах можно записать аккуратно как

${ Displaystyle { begin {выровнено} & left [L left ( alpha ^ {A}, { alpha ^ {A}} _ {, nu}, x ^ { mu} right) -L left ( varphi ^ {A}, { varphi ^ {A}} _ {, nu}, x ^ { mu} right) right] [4pt] = {} & { frac { partial} { partial x ^ { sigma}}} left ({ frac { partial L} { partial { varphi ^ {A}} _ {, sigma}}} right) { bar { delta}} varphi ^ {A} + { frac { partial L} { partial { varphi ^ {A}} _ {, sigma}}} { bar { delta}} { varphi ^ {A}} _ {, sigma} = { frac { partial} { partial x ^ { sigma}}} left ({ frac { partial L} { partial { varphi ^ {A }} _ {, sigma}}} { bar { delta}} varphi ^ {A} right). end {выравнивается}}}$

Таким образом, изменение действия можно записать как

${ displaystyle int _ { Omega} { frac { partial} { partial x ^ { sigma}}} left {{ frac { partial L} { partial { varphi ^ {A} } _ {, sigma}}} { bar { delta}} varphi ^ {A} + L left ( varphi ^ {A}, { varphi ^ {A}} _ {, nu}, x ^ { mu} right) delta x ^ { sigma} right } d ^ {4} x = 0 ,.}$

Поскольку это верно для любой области Ω, подынтегральное выражение должно быть нулевым.

${ displaystyle { frac { partial} { partial x ^ { sigma}}} left {{ frac { partial L} { partial { varphi ^ {A}} _ {, sigma} }} { bar { delta}} varphi ^ {A} + L left ( varphi ^ {A}, { varphi ^ {A}} _ {, nu}, x ^ { mu} right) delta x ^ { sigma} right } = 0 ,.}$

Для любого сочетания различных симметрия преобразований, возмущение можно записать

${ displaystyle delta x ^ { mu} = varepsilon X ^ { mu}}$

${ displaystyle delta varphi ^ {A} = varepsilon Psi ^ {A} = { bar { delta}} varphi ^ {A} + varepsilon { mathcal {L}} _ {X} varphi ^ {A}}$

куда ${ Displaystyle { mathcal {L}} _ {X} varphi ^ {A}}$ это Производная Ли из φ^А в Икс^μ направление. Когда φ^А скаляр или ${ displaystyle {X ^ { mu}} _ {, nu} = 0}$,

${ displaystyle { mathcal {L}} _ {X} varphi ^ {A} = { frac { partial varphi ^ {A}} { partial x ^ { mu}}} X ^ { mu } ,.}$

Из этих уравнений следует, что вариация поля, взятая в одной точке, равна

${ displaystyle { bar { delta}} varphi ^ {A} = varepsilon Psi ^ {A} - varepsilon { mathcal {L}} _ {X} varphi ^ {A} ,.}$

Дифференцируя указанное выше расхождение относительно ε в ε = 0 и изменение знака приводит к закону сохранения

${ displaystyle { frac { partial} { partial x ^ { sigma}}} j ^ { sigma} = 0}$

где сохраняющийся ток равен

${ displaystyle j ^ { sigma} = left [{ frac { partial L} { partial { varphi ^ {A}} _ {, sigma}}} { mathcal {L}} _ {X } varphi ^ {A} -L , X ^ { sigma} right] - left ({ frac { partial L} { partial { varphi ^ {A}} _ {, sigma}} } right) Psi ^ {A} ,.}$

Вывод коллекторов / пучков волокон

Предположим, у нас есть п-размерно ориентированный Риманово многообразие, M и целевой коллектор Т. Позволять ${ displaystyle { mathcal {C}}}$ быть конфигурационное пространство из гладкие функции из M к Т. (В общем, у нас могут быть гладкие участки пучок волокон над M.)

Примеры этого M по физике включают:

• В классическая механика, в Гамильтониан формулировка M - одномерное многообразие ${ Displaystyle mathbb {R}}$, представляющий время, а целевым пространством является котангенсный пучок из Космос обобщенных позиций.
• В теория поля, M это пространство-время многообразие и целевое пространство - это набор значений, которые поля могут принимать в любой заданной точке. Например, если есть м настоящий -ценный скалярные поля, ${ displaystyle varphi _ {1}, ldots, varphi _ {m}}$, то целевое многообразие ${ Displaystyle mathbb {R} ^ {m}}$. Если поле является вещественным векторным полем, то целевое многообразие изоморфный к ${ Displaystyle mathbb {R} ^ {3}}$.

Теперь предположим, что есть функциональный

${ displaystyle { mathcal {S}}: { mathcal {C}} rightarrow mathbb {R},}$

называется действие. (Он принимает значения в ${ Displaystyle mathbb {R}}$, скорее, чем ${ Displaystyle mathbb {C}}$; это по физическим причинам и не имеет значения для данного доказательства.)

Чтобы добраться до обычной версии теоремы Нётер, нам потребуются дополнительные ограничения на действие. Мы предполагаем ${ Displaystyle { mathcal {S}} [ varphi]}$ это интеграл над M функции

${ Displaystyle { mathcal {L}} ( varphi, partial _ { mu} varphi, x)}$

называется Плотность лагранжиана, в зависимости от φ, это производная и положение. Другими словами, для φ в ${ displaystyle { mathcal {C}}}$

${ displaystyle { mathcal {S}} [ varphi] , = , int _ {M} { mathcal {L}} [ varphi (x), partial _ { mu} varphi (x ), x] , d ^ {n} x.}$

Предположим, нам даны граничные условия, т.е. указание значения φ на граница если M является компактный, или какое-то ограничение на φ в качестве Икс приближается к ∞. Тогда подпространство из ${ Displaystyle { mathcal {C}}}$ состоящий из функций φ так что все функциональные производные из ${ Displaystyle { mathcal {S}}}$ в φ равны нулю, то есть:

${ displaystyle { frac { delta { mathcal {S}} [ varphi]} { delta varphi (x)}} приблизительно 0}$

и это φ удовлетворяет заданным граничным условиям, является подпространством на оболочке решения. (Видеть принцип стационарного действия )

Теперь предположим, что у нас есть бесконечно малое преобразование на ${ Displaystyle { mathcal {C}}}$, порожденный функциональный происхождение, Q такой, что

${ Displaystyle Q left [ int _ {N} { mathcal {L}} , mathrm {d} ^ {n} x right] приблизительно int _ { partial N} f ^ { mu } [ varphi (x), partial varphi, partial partial varphi, ldots] , ds _ { mu}}$

для всех компактных подмногообразий N или другими словами,

${ Displaystyle Q [{ mathcal {L}} (x)] приблизительно partial _ { mu} f ^ { mu} (x)}$

для всех Икс, где мы положили

${ displaystyle { mathcal {L}} (x) = { mathcal {L}} [ varphi (x), partial _ { mu} varphi (x), x].}$

Если это имеет место на оболочке и вне оболочки, мы говорим Q генерирует симметрию вне оболочки. Если это только так на оболочке, мы говорим Q создает симметрию на оболочке. Затем мы говорим Q является генератором один параметр симметрия Группа Ли.

Теперь для любого N, из-за Эйлер – Лагранж теорема на оболочке (и только на оболочке), у нас есть

${ displaystyle { begin {align} Q left [ int _ {N} { mathcal {L}} , mathrm {d} ^ {n} x right] & = int _ {N} left [{ frac { partial { mathcal {L}}} { partial varphi}} - partial _ { mu} { frac { partial { mathcal {L}}} { partial ( partial _ { mu} varphi)}} right] Q [ varphi] , mathrm {d} ^ {n} x + int _ { partial N} { frac { partial { mathcal {L }}} { partial ( partial _ { mu} varphi)}} Q [ varphi] , mathrm {d} s _ { mu} & приблизительно int _ { partial N} f ^ { mu} , mathrm {d} s _ { mu}. end {выравнивается}}}$

Поскольку это верно для любого N, у нас есть

${ displaystyle partial _ { mu} left [{ frac { partial { mathcal {L}}} { partial ( partial _ { mu} varphi)}} Q [ varphi] -f ^ { mu} right] приблизительно 0.}$

Но это уравнение неразрывности для текущего ${ Displaystyle J ^ { mu}}$ определяется:^[12]

${ Displaystyle J ^ { mu} , = , { frac { partial { mathcal {L}}} { partial ( partial _ { mu} varphi)}} Q [ varphi] - е ^ { mu},}$

который называется Ток Нётер связанный с симметрия. Уравнение неразрывности говорит нам, что если мы интегрировать этот ток над космический ломтик, получаем сохраненное количество называется зарядом Нётер (при условии, конечно, если M некомпактен, токи достаточно быстро спадают на бесконечности).

Комментарии

Теорема Нётер - это на оболочке Теорема: она основана на использовании уравнений движения - классической траектории. Он отражает связь между граничными условиями и вариационным принципом. Если в действии нет граничных членов, из теоремы Нётер следует, что

${ displaystyle int _ { partial N} J ^ { mu} ds _ { mu} приблизительно 0.}$

Квантовые аналоги теоремы Нётер, включающие математические ожидания, например ${ displaystyle left langle int d ^ {4} x ~ partial cdot { textbf {J}} right rangle = 0}$, зондирование вне оболочки количества также являются Личности Уорда-Такахаши.

Обобщение на алгебры Ли

Предположим, у нас есть два вывода симметрии Q₁ и Q₂. Потом, [Q₁, Q₂] также является выводом симметрии. Посмотрим на это подробно. Скажем

${ Displaystyle Q_ {1} [{ mathcal {L}}] приблизительно partial _ { mu} f_ {1} ^ { mu}}$

и

${ Displaystyle Q_ {2} [{ mathcal {L}}] приблизительно partial _ { mu} f_ {2} ^ { mu}}$

Потом,

${ displaystyle [Q_ {1}, Q_ {2}] [{ mathcal {L}}] = Q_ {1} [Q_ {2} [{ mathcal {L}}]] - Q_ {2} [Q_ {1} [{ mathcal {L}}]] приблизительно partial _ { mu} f_ {12} ^ { mu}}$

куда ж₁₂ = Q₁[ж₂^μ] − Q₂[ж₁^μ]. Так,

${ displaystyle j_ {12} ^ { mu} = left ({ frac { partial} { partial ( partial _ { mu} varphi)}} { mathcal {L}} right) ( Q_ {1} [Q_ {2} [ varphi]] - Q_ {2} [Q_ {1} [ varphi]]) - f_ {12} ^ { mu}.}$

Это показывает, что мы можем естественным образом распространить теорему Нётер на большие алгебры Ли.

Обобщение доказательства

Это относится к любой вывод локальной симметрии Q удовлетворение QS ≈ 0, а также к более общим локальным функционально дифференцируемым действиям, в том числе к тем, в которых лагранжиан зависит от высших производных полей. Позволять ε - произвольная гладкая функция пространственно-временного (или временного) многообразия такая, что замыкание ее носителя не пересекается с границей. ε это функция тестирования. Тогда из-за вариационного принципа (который нет к границе, кстати), деривационное распределение q, порожденное q[ε] [Φ (Икс)] = ε(Икс)Q[Φ (Икс)] удовлетворяет q[ε][S] ≈ 0 для каждогоε, или более компактно, q(Икс)[S] ≈ 0 для всех Икс не на границе (но помните, что q(Икс) является сокращением для вывода распределение, а не вывод, параметризованный Икс в целом). Это обобщение теоремы Нётер.

Чтобы увидеть, как обобщение связано с версией, приведенной выше, предположим, что действие - это пространственно-временной интеграл лагранжиана, который зависит только от φ и его первых производных. Также предположим

${ Displaystyle Q [{ mathcal {L}}] приблизительно partial _ { mu} f ^ { mu}}$

Потом,

${ displaystyle { begin {align} q [ varepsilon] [{ mathcal {S}}] & = int q [ varepsilon] [{ mathcal {L}}] d ^ {n} x [ 6pt] & = int left { left ({ frac { partial} { partial varphi}} { mathcal {L}} right) varepsilon Q [ varphi] + left [{ frac { partial} { partial ( partial _ { mu} varphi)}} { mathcal {L}} right] partial _ { mu} ( varepsilon Q [ varphi]) right } d ^ {n} x [6pt] & = int left { varepsilon Q [{ mathcal {L}}] + partial _ { mu} varepsilon left [{ frac { partial} { partial left ( partial _ { mu} varphi right)}} { mathcal {L}} right] Q [ varphi] right } , d ^ {n} x [6pt] & приблизительно int varepsilon partial _ { mu} left {f ^ { mu} - left [{ frac { partial} { partial ( partial _ { mu} varphi)}} { mathcal {L}} right] Q [ varphi] right } , d ^ {n} x end {выровнено}}}$

для всех ${ displaystyle varepsilon}$.

В более общем смысле, если лагранжиан зависит от высших производных, то

${ displaystyle { begin {align} partial _ { mu} left [е ^ { mu} - left [{ frac { partial} { partial ( partial _ { mu} varphi) }} { mathcal {L}} right] right. & left.Q [ varphi] -2 left [{ frac { partial} { partial ( partial _ { mu} partial _ { nu} varphi)}} { mathcal {L}} right] partial _ { nu} Q [ varphi] right. [6pt] & left. {} + partial _ { nu} left [ left [{ frac { partial} { partial ( partial _ { mu} partial _ { nu} varphi)}} { mathcal {L}} right] Q [ varphi] right] - , cdots right] приблизительно 0. end {align}}}$

Примеры

Пример 1: Сохранение энергии

Рассмотрим частный случай ньютоновской частицы массы м, координировать Икс, движущиеся под действием потенциальной V, согласованный по времени т. В действие, S, является:

${ Displaystyle { begin {align} { mathcal {S}} [x] & = int L [x (t), { dot {x}} (t)] , dt & = int left ({ frac {m} {2}} sum _ {i = 1} ^ {3} { dot {x}} _ {i} ^ {2} -V (x (t)) right ) , дт. конец {выровнено}}}$

Первый член в скобках - это кинетическая энергия частицы, а вторая - ее потенциальная энергия. Рассмотрим генератор переводы времени Q = д / дт. Другими словами, ${ Displaystyle Q [х (т)] = { точка {х}} (т)}$. Координата Икс имеет явную зависимость от времени, в то время как V не; как следствие:

${ displaystyle Q [L] = m sum _ {i} { dot {x}} _ {i} { ddot {x}} _ {i} - sum _ {i} { frac { partial V (x)} { partial x_ {i}}} { dot {x}} _ {i} = { frac {d} {dt}} left [{ frac {m} {2}} сумма _ {i} { dot {x}} _ {i} ^ {2} -V (x) right]}$

так что мы можем установить

${ displaystyle L = { frac {m} {2}} sum _ {i} { dot {x}} _ {i} ^ {2} -V (x).}$

Потом,

${ displaystyle { begin {align} j & = sum _ {i = 1} ^ {3} { frac { partial L} { partial { dot {x}} _ {i}}} Q [x_ {i}] - L & = m sum _ {i} { dot {x}} _ {i} ^ {2} - left [{ frac {m} {2}} sum _ { i} { dot {x}} _ {i} ^ {2} -V (x) right] & = { frac {m} {2}} sum _ {i} { dot {x }} _ {i} ^ {2} + V (x). end {align}}}$

Правая часть - это энергия, и теорема Нётер утверждает, что ${ displaystyle { dot {j}} = 0}$ (т.е. принцип сохранения энергии является следствием инвариантности относительно временных трансляций).

В более общем смысле, если лагранжиан не зависит явно от времени, величина

${ displaystyle sum _ {i = 1} ^ {3} { frac { partial L} { partial { dot {x}} _ {i}}} { dot {x_ {i}}} - L}$

(называется Гамильтониан ) сохраняется.

Пример 2: Сохранение центра импульса

Продолжая рассматривать одномерное время, пусть

${ displaystyle { begin {align} { mathcal {S}} [{ vec {x}}] & = int { mathcal {L}} [{ vec {x}} (t), { точка { vec {x}}} (t)] dt [6pt] & = int left [ sum _ { alpha = 1} ^ {N} { frac {m _ { alpha}} { 2}} ({ dot { vec {x}}} _ { alpha}) ^ {2} - sum _ { alpha < beta} V _ { alpha beta} ({ vec {x} } _ { beta} - { vec {x}} _ { alpha}) right] dt, end {align}}}$