Оценка плотности - Density estimation
Эта статья нужны дополнительные цитаты для проверка. (Август 2012 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
В вероятность и статистика,оценка плотности это построение оценивать на основе наблюдаемых данные ненаблюдаемого базового функция плотности вероятности. Под ненаблюдаемой функцией плотности понимается плотность, в соответствии с которой распределяется большая популяция; данные обычно рассматриваются как случайная выборка из этой совокупности.
Используются различные подходы к оценке плотности, в том числе Окна парзен и ряд кластеризация данных методы, в том числе векторное квантование. Самая основная форма оценки плотности - это масштабированный гистограмма.
Пример оценки плотности
Мы рассмотрим записи о заболеваемости сахарный диабет. Следующее дословно цитируется из набор данных описание:
- Популяция женщин в возрасте от 21 года Пима Индийское наследие и жизнь недалеко от Феникса, штат Аризона, были проверены на сахарный диабет в соответствии с Всемирная организация здоровья критерии. Данные были собраны Национальным институтом диабета, болезней органов пищеварения и почек США. Мы использовали 532 полных записи.[1][2]
В этом примере мы строим три оценки плотности для "glu" (плазма глюкоза концентрация), один условный при наличии диабета, второе - при условии отсутствия диабета, а третье - при отсутствии диабета. Затем оценки условной плотности используются для построения вероятности диабета, обусловленного «glu».
Данные "glu" были получены из пакета MASS.[3] из Язык программирования R. Внутри R ? Pima.tr и ? Pima.te дать более полный отчет о данных.
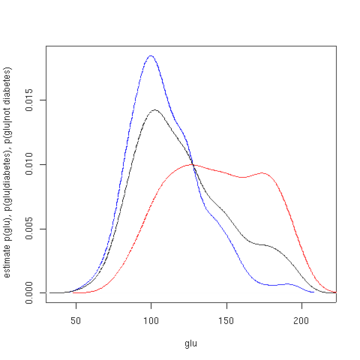
В иметь в виду «glu» в случаях диабета составляет 143,1, а стандартное отклонение составляет 31,26. Среднее значение «glu» в случаях, не связанных с диабетом, составляет 110,0, а стандартное отклонение составляет 24,29. Из этого мы видим, что в этом наборе данных диабет Случаи связаны с более высокими уровнями "glu". Это будет более понятно с помощью графиков оцененных функций плотности.
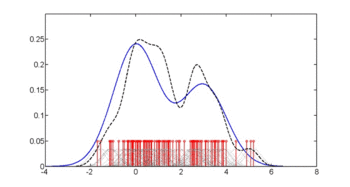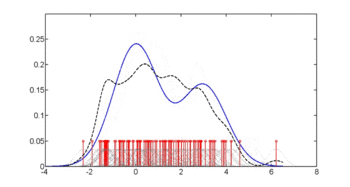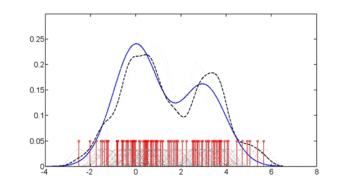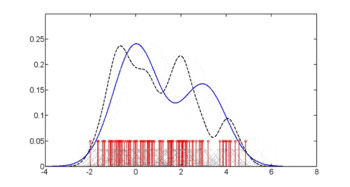
На первом рисунке показаны оценки плотности п(глю | диабет = 1), п(глю | диабет = 0) и п(glu) .Оценки плотности представляют собой оценки ядерной плотности с использованием гауссова ядра. То есть функция плотности Гаусса помещается в каждую точку данных, и сумма функций плотности вычисляется по диапазону данных.
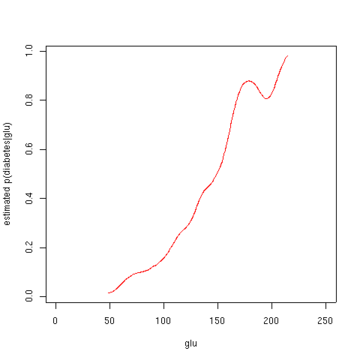
Из плотности "glu", обусловленной диабетом, мы можем получить вероятность диабета, обусловленного "glu", через Правило Байеса. Для краткости «диабет» сокращенно обозначается как «дб». в этой формуле.
На втором рисунке показана оценка апостериорной вероятности п(диабет = 1 | глю). Из этих данных видно, что повышенный уровень «глю» связан с диабетом.
Скрипт например
Следующие команды R создадут фигуры, показанные выше. Эти команды можно вводить в командной строке с помощью вырезания и вставки.
библиотека(МАССА)данные(Pima.tr)данные(Pima.te)Пима <- rbind (Pima.tr, Pima.te)глю <- Пима [, 'глю']d0 <- Пима [, 'тип'] == 'Нет'd1 <- Пима [, 'тип'] == 'Да'base.rate.d1 <- сумма(d1) / (сумма(d1) + сумма(d0))гл. плотность <- плотность (глю)гл.д0.плотность <- плотность (glu [d0])гл.д1.плотность <- плотность (glu [d1])glu.d0.f <- приблизительно(гл.д0.плотность$Икс, гл.д0.плотность$у)glu.d1.f <- приблизительно(гл.д1.плотность$Икс, гл.д1.плотность$у)p.d.given.glu <- функция(глю, base.rate.d1){ p1 <- glu.d1.f(глю) * base.rate.d1 p0 <- glu.d0.f(глю) * (1 - base.rate.d1) p1 / (p0 + p1)}Икс <- 1:250у <- p.d.given.glu (Икс, base.rate.d1)участок(Икс, у, тип='l', Col='красный', xlab='глю', ylab='оценка p (диабет | glu)')участок(плотность(glu [d0]), Col='синий', xlab='глю', ylab='оценка p (glu), p (glu | диабет), p (glu | не диабет) ', главный=NA)линии(плотность(glu [d1]), Col='красный')Обратите внимание, что в приведенном выше средстве оценки условной плотности используются полосы пропускания, оптимальные для безусловных плотностей. В качестве альтернативы можно использовать метод Холла, Расина и Ли (2004).[4] и пакет R np[5]для автоматического (управляемого данными) выбора полосы пропускания, оптимальной для оценок условной плотности; увидеть виньетку НП[6] для знакомства с пакетом np. Следующие команды R используют npcdens () функция для обеспечения оптимального сглаживания. Обратите внимание, что ответ «Да» / «Нет» является фактором.
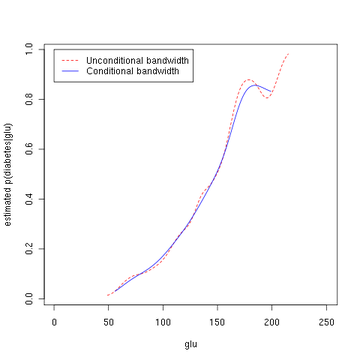
библиотека(нп)fy.x <- npcdens(тип~глю, nmulti=1, данные=Пима)Pima.eval <- data.frame(тип=фактор("Да"), глю=seq(мин(Пима$глю), Максимум(Пима$глю), длина=250)) участок(Икс, у, тип='l', lty=2, Col='красный', xlab='глю', ylab='оценка p (диабет | glu)')линии(Pima.eval$глю, предсказывать(fy.x, новые данные=Pima.eval), Col="синий")легенда(0, 1, c(«Безусловная пропускная способность», «Условная пропускная способность»), Col=c("красный", "синий"), lty=c(2, 1))На третьем рисунке используется оптимальное сглаживание методом Холла, Расина и Ли.[4] это указывает на то, что ширина полосы безусловной плотности, использованная на втором рисунке выше, дает оценку условной плотности, которая может быть несколько не сглажена.
Применение и цель
Очень естественное использование оценок плотности - неформальное исследование свойств данного набора данных. Оценки плотности могут дать ценную информацию о таких характеристиках, как асимметрия и многомодальность данных. В некоторых случаях они сделают выводы, которые затем могут быть расценены как самоочевидно верные, в то время как в других они просто укажут путь для дальнейшего анализа и / или сбора данных.[7]

Важным аспектом статистики часто является представление данных клиенту для объяснения и иллюстрации выводов, которые могли быть получены другими способами. Для этой цели идеально подходят оценки плотности по той простой причине, что они довольно легко понятны не математикам.
Еще несколько примеров, иллюстрирующих использование оценок плотности для исследовательских и презентационных целей, включая важный случай двумерных данных.[9]
Оценка плотности также часто используется в обнаружение аномалии или же обнаружение новизны:[10] если наблюдение находится в области очень низкой плотности, это, вероятно, аномалия или новинка.
- В гидрология то гистограмма и оценочная функция плотности данных об осадках и речном расходе, проанализированная с помощью распределение вероятностей, используются, чтобы получить представление об их поведении и частоте появления.[11] Пример показан на синем рисунке.
Смотрите также
- Оценка плотности ядра
- Средняя квадратичная ошибка
- Гистограмма
- Оценка многомерной плотности ядра
- Оценка спектральной плотности
- Встраивание распределений в ядро
- Генеративная модель
- Применение статистики заказов: непараметрическая оценка плотности
- Подгонка распределения вероятностей
Рекомендации
- ^ «Диабет у женщин индейцев пима - R-документация».
- ^ Смит, Дж. У., Эверхарт, Дж. Э., Диксон, У. К., Ноулер, У. К. и Йоханнес, Р. С. (1988). Р. А. Гринс (ред.). «Использование алгоритма обучения ADAP для прогнозирования начала сахарного диабета». Труды симпозиума по компьютерным приложениям в медицине (Вашингтон, 1988 г.). Лос-Аламитос, Калифорния: 261–265. ЧВК 2245318.CS1 maint: несколько имен: список авторов (связь)
- ^ «Функции поддержки и наборы данных для Venables и Ripley's MASS».
- ^ а б Питер Холл; Джеффри С. Расин; Ци Ли (2004). «Перекрестная проверка и оценка условной плотности вероятностей». Журнал Американской статистической ассоциации. 99 (468): 1015–1026. CiteSeerX 10.1.1.217.93. Дои:10.1198/016214504000000548.
- ^ «Пакет np - пакет R, который предоставляет множество непараметрических и полупараметрических методов ядра, которые беспрепятственно обрабатывают сочетание непрерывных, неупорядоченных и упорядоченных типов данных факторов».
- ^ Тристен Хейфилд; Джеффри С. Расин. "Пакет НП" (PDF).
- ^ Сильверман, Б. В. (1986). Оценка плотности для статистики и анализа данных. Чепмен и Холл. ISBN 978-0412246203.
- ^ Калькулятор вероятностных распределений и функций плотности
- ^ Джеф Х., Гивенс (2013). Вычислительная статистика. Вайли. п. 330. ISBN 978-0-470-53331-4.
- ^ Pimentel, Marco A.F .; Клифтон, Дэвид А .; Клифтон, Лей; Тарасенко, Лионель (2 января 2014 г.). «Обзор обнаружения новинок». Обработка сигналов. 99 (Июнь 2014 г.): 215–249. Дои:10.1016 / j.sigpro.2013.12.026.
- ^ Иллюстрация гистограмм и функций плотности вероятности
Источники
- Брайан Д. Рипли (1996). Распознавание образов и нейронные сети. Кембридж: Издательство Кембриджского университета. ISBN 978-0521460866.
- Тревор Хасти, Роберт Тибширани, и Джером Фридман. Элементы статистического обучения. Нью-Йорк: Спрингер, 2001. ISBN 0-387-95284-5. (См. Главу 6.)
- Ци Ли и Джеффри С. Расин. Непараметрическая эконометрика: теория и практика. Издательство Принстонского университета, 2007 г., ISBN 0-691-12161-3. (См. Главу 1.)
- Д.В. Скотт. Многомерная оценка плотности. Теория, практика и визуализация. Нью-Йорк: Wiley, 1992.
- B.W. Сильверман. Оценка плотности. Лондон: Чепмен и Холл, 1986. ISBN 978-0-412-24620-3
внешняя ссылка
- CREEM: Центр исследований в области экологического и экологического моделирования Загрузки для бесплатных пакетов программного обеспечения для оценки плотности Расстояние 4 (из Исследовательского отдела по оценке популяции диких животных «RUWPA») и WiSP.
- Сводка содержимого репозитория машинного обучения UCI (Исходный набор данных из 732 записей и дополнительные примечания см. В «Базе данных диабета индейцев пима».)
- Код MATLAB для одномерный и двумерный оценка плотности
- libAGF Программное обеспечение C ++ для оценка плотности переменного ядра.

