Классическая механика - Classical mechanics

Часть серии по
Классическая механика
${displaystyle {extbf {F}} = {гидроразрыв {d} {dt}} (m {extbf {v}})}$ Второй закон движения
История График Учебники
ветви Применяемый Небесный Continuum Динамика Кинематика Кинетика Статика Статистический
Основы Ускорение Угловой момент Пара Принцип Даламбера Энергия кинетический потенциал Сила Точка зрения Инерциальная система отсчета Импульс Инерция  / Момент инерции Масса Механическая мощность Механическая работа Момент Импульс Космос Скорость Время Крутящий момент Скорость Виртуальная работа
Составы Законы движения Ньютона Аналитическая механика Лагранжева механика Гамильтонова механика Рутианская механика Уравнение Гамильтона – Якоби Уравнение движения Аппеля Механика Купмана – фон Неймана
Основные темы Демпфирование  (соотношение ) Смещение Уравнения движения Законы движения Эйлера Фиктивная сила Трение Гармонический осциллятор Инерционный  / Неинерциальная система отсчета Механика движения плоских частиц Движение  (линейный ) Закон всемирного тяготения Ньютона Законы движения Ньютона Относительная скорость Жесткое тело динамика Уравнения Эйлера Простые гармонические колебания Вибрация
Вращение Круговое движение Вращающаяся опорная рамка Центростремительная сила Центробежная сила реактивный Сила Кориолиса Маятник Тангенциальная скорость Скорость вращения Угловое ускорение  / смещение  / частота  / скорость
Ученые Кеплер Галилео Гюйгенс Ньютон Хоррокс Галлей Даниэль Бернулли Иоганн Бернулли Эйлер д'Аламбер Clairaut Лагранж Лаплас Гамильтон Пуассон Коши Раут Liouville Appell Гиббс Купман фон Нейман
Категории ► Классическая механика

Схема орбитального движения спутника вокруг Земли, показывающая перпендикулярные векторы скорости и ускорения (силы).

Классический^{[примечание 1]} механика это физическая теория описывая движение из макроскопический объекты, из снаряды к частям машины, и астрономические объекты, Такие как космический корабль, планеты, звезды и галактики. Для объектов, управляемых классической механикой, если текущее состояние известно, можно предсказать, как оно будет двигаться в будущем (детерминизм) и как оно двигалось в прошлом (обратимость).

Самое раннее развитие классической механики часто называют механикой Ньютона. Он состоит из используемых физических понятий и математических методов, изобретенных Исаак Ньютон, Готфрид Вильгельм Лейбниц и другие в 17 веке, чтобы описать движение тела под влиянием системы силы. Позже были разработаны более абстрактные методы, которые привели к переформулировке классической механики, известной как Лагранжева механика и Гамильтонова механика. Эти достижения, сделанные в основном в 18-19 веках, существенно выходят за рамки работ Ньютона, особенно благодаря использованию в них аналитическая механика. Они, с некоторыми изменениями, также используются во всех областях современной физики.

Классическая механика обеспечивает чрезвычайно точные результаты при изучении больших объектов, не очень массивных и скоростных, не приближающихся к скорость света. Когда исследуемые объекты имеют размер диаметра атома, возникает необходимость ввести другое основное подполе механика: квантовая механика. Чтобы описать скорости, которые не малы по сравнению со скоростью света, специальная теория относительности необходим. В случаях, когда объекты становятся чрезвычайно массивными, общая теория относительности становится применимым. Однако ряд современных источников действительно включает релятивистскую механику в классическую физику, которая, по их мнению, представляет классическую механику в ее наиболее развитой и точной форме.

Описание теории

Анализ движение снаряда является частью классической механики.

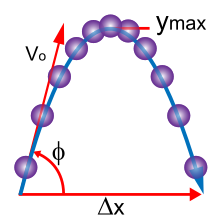
Ниже представлены основные понятия классической механики. Для простоты он часто моделирует объекты реального мира как точечные частицы (предметы незначительного размера). Движение точечной частицы характеризуется малым числом параметры: его позиция, масса, а силы применяется к нему. Каждый из этих параметров обсуждается по очереди.

В действительности, объекты, которые может описать классическая механика, всегда имеют ненулевой размер. (Физика очень мелкие частицы, такие как электрон, более точно описывается квантовая механика.) Объекты с ненулевым размером имеют более сложное поведение, чем гипотетические точечные частицы, из-за дополнительных степени свободы, например, бейсбол может вращение пока он движется. Однако результаты для точечных частиц можно использовать для изучения таких объектов, рассматривая их как составной объекты, состоящие из большого количества коллективно действующих точечных частиц. В центр массы составного объекта ведет себя как точечная частица.

Классическая механика использует здравый смысл представления о том, как материя и силы существуют и взаимодействуют. Предполагается, что материя и энергия имеют определенные, познаваемые атрибуты, такие как местоположение в пространстве и скорость. Нерелятивистская механика также предполагает, что силы действуют мгновенно (см. Также Действия на расстоянии ).

Позиция и ее производные

В позиция из точечная частица определяется относительно система координат с центром в произвольной фиксированной точке отсчета в Космос назвал происхождение О. Простая система координат могла бы описать положение частица п с вектор помечен стрелкой, обозначенной р что указывает из начала О В точку п. В общем, точечная частица не обязательно должна быть неподвижной относительно О. В случаях, когда п движется относительно О, р определяется как функция т, время. В доэйнштейновской теории относительности (известной как Галилея относительность ) время считается абсолютным, т.е. временной интервал то, что наблюдается между любой данной парой событий, одинаково для всех наблюдателей.^[3] Помимо полагаться на абсолютное время, классическая механика предполагает Евклидова геометрия для структуры пространства.^[4]

Скорость и скорость

В скорость, или скорость изменения положения во времени, определяется как производная позиции по времени:

${displaystyle mathbf {v} = {mathrm {d} mathbf {r} вместо mathrm {d} t} ,!}$.

В классической механике скорости бывают непосредственно аддитивными и вычитающими. Например, если одна машина движется на восток со скоростью 60 км / ч и обгоняет другую машину, движущуюся в том же направлении со скоростью 50 км / ч, более медленная машина воспринимает более быструю машину как движущуюся на восток на 60-50 = 10 км / ч. Однако с точки зрения более быстрого автомобиля более медленный автомобиль движется на 10 км / ч на запад, что часто обозначается как -10 км / ч, где знак указывает на противоположное направление. Скорости складываются напрямую как векторные величины; с ними нужно бороться, используя векторный анализ.

Математически, если скорость первого объекта в предыдущем обсуждении обозначена вектором ты = тыd а скорость второго объекта - вектором v = vе, куда ты - скорость первого объекта, v - скорость второго объекта, а d и е находятся единичные векторы в направлениях движения каждого объекта соответственно, то скорость первого объекта, видимого вторым объектом, равна

${displaystyle mathbf {u} '= mathbf {u} -mathbf {v},.}$

Точно так же первый объект видит скорость второго объекта как

${displaystyle mathbf {v '} = mathbf {v} -mathbf {u},.}$

Когда оба объекта движутся в одном направлении, это уравнение можно упростить до

${displaystyle mathbf {u} '= (u-v) mathbf {d},.}$

Или, игнорируя направление, разница может быть выражена только в скорости:

${displaystyle u '= u-v ,.}$

Ускорение

В ускорение, или скорость изменения скорости, является производная скорости по времени ( вторая производная позиции по времени):

${displaystyle mathbf {a} = {mathrm {d} mathbf {v} over mathrm {d} t} = {mathrm {d ^ {2}} mathbf {r} over mathrm {d} t ^ {2}}.}$

Ускорение представляет собой изменение скорости во времени. Скорость может изменяться либо по величине, либо по направлению, либо по обоим направлениям. Иногда уменьшение величины скорости "v" упоминается как замедление, но обычно любое изменение скорости с течением времени, включая замедление, называется просто ускорением.

Справочные рамки

В то время как положение, скорость и ускорение частица можно описать относительно любого наблюдатель в любом состоянии движения классическая механика предполагает существование особого семейства системы отсчета в котором механические законы природы принимают сравнительно простую форму. Эти специальные системы отсчета называются инерциальные системы отсчета. Инерциальная система отсчета - это идеализированная система отсчета, в которой объект не имеет внешней силы, действующей на него. Поскольку на него не действует внешняя сила, объект имеет постоянную скорость; то есть он либо находится в состоянии покоя, либо движется равномерно по прямой линии.

Ключевым понятием инерциальных систем отсчета является метод их идентификации. Для практических целей системы отсчета, которые не ускоряются относительно далекие звезды (очень удаленная точка) считаются хорошими приближениями к инерциальной системе отсчета. Неинерциальные системы отсчета ускоряться по отношению к существующей инерциальной системе отсчета. Они составляют основу теории относительности Эйнштейна. Из-за относительного движения частицы в неинерциальной системе отсчета кажутся движущимися способами, не объясняемыми силами существующих полей в системе отсчета. Следовательно, похоже, что существуют другие силы, которые входят в уравнения движения исключительно в результате относительного ускорения. Эти силы называются фиктивные силы, силы инерции или псевдосилы.

Рассмотрим два системы отсчета S и S '. Для наблюдателей в каждой из систем отсчета событие имеет пространственно-временные координаты (Икс,у,z,т) в кадре S и (Икс',y ',z ',т ') в кадре S '. Предполагая, что время измеряется одинаково во всех системах отсчета, и если мы требуем Икс = Икс' когда т = 0, то связь между пространственно-временными координатами одного и того же события, наблюдаемого из системы отсчета S ' и S, которые движутся с относительной скоростью ты в Икс направление:

${displaystyle x '= x-ut,}$

${displaystyle y '= y,}$

${displaystyle z '= z,}$

${displaystyle t '= t ,.}$

Этот набор формул определяет групповое преобразование известный как Преобразование Галилея (неофициально Преобразование Галилея). Эта группа является предельным случаем Группа Пуанкаре используется в специальная теория относительности. Предельный случай применяется, когда скорость ты очень маленький по сравнению с c, то скорость света.

Преобразования имеют следующие последствия:

• v′ = v − ты (скорость v′ Частицы с точки зрения S'Медленнее на ты чем его скорость v с точки зрения S)
• а′ = а (ускорение частицы одинаково в любой инерциальной системе отсчета)
• F′ = F (сила, действующая на частицу, одинакова в любой инерциальной системе отсчета)
• то скорость света не является константой в классической механике, равно как и особое положение, придаваемое скорости света в релятивистская механика есть аналог в классической механике.

Для некоторых задач удобно использовать вращающиеся координаты (системы отсчета). Таким образом, можно либо сохранить отображение в удобную инерциальную систему отсчета, либо ввести дополнительно фиктивную центробежная сила и Сила Кориолиса.

Силы; Второй закон Ньютона

Сила в физике - это любое действие, которое вызывает изменение скорости объекта; то есть ускориться. Сила исходит изнутри поле, например, электростатическое поле (вызванное статическими электрическими зарядами), электромагнитное поле (вызванное движущимися зарядами) или гравитационное поле (вызванное массой) и другие.

Ньютон был первым, кто математически выразил взаимосвязь между сила и импульс. Некоторые физики интерпретируют Второй закон движения Ньютона как определение силы и массы, в то время как другие считают его фундаментальным постулатом, законом природы.^[5] Любая интерпретация имеет одни и те же математические последствия, исторически известные как «Второй закон Ньютона»:

${displaystyle mathbf {F} = {mathrm {d} mathbf {p} over mathrm {d} t} = {mathrm {d} (mmathbf {v}) over mathrm {d} t}.}$

Количество мv называется (канонический ) импульс. Таким образом, результирующая сила, действующая на частицу, равна скорости изменения импульса частицы со временем. Поскольку определение ускорения а = dv/ дт, второй закон можно записать в упрощенной и более привычной форме:

${displaystyle mathbf {F} = mmathbf {a},.}$

Пока известна сила, действующая на частицу, второго закона Ньютона достаточно для описания движения частицы. Как только станут доступны независимые соотношения для каждой силы, действующей на частицу, их можно подставить во второй закон Ньютона, чтобы получить обыкновенное дифференциальное уравнение, который называется уравнение движения.

В качестве примера предположим, что трение - единственная сила, действующая на частицу, и что ее можно смоделировать как функцию скорости частицы, например:

${displaystyle mathbf {F} _ {m {R}} = - lambda mathbf {v} ,,}$

куда λ - положительная константа, отрицательный знак означает, что сила противоположна направлению скорости. Тогда уравнение движения имеет вид

${displaystyle -lambda mathbf {v} = mmathbf {a} = m {mathrm {d} mathbf {v} вместо mathrm {d} t} ,.}$

Это может быть интегрированный чтобы получить

${displaystyle mathbf {v} = mathbf {v} _ {0} e ^ {frac {-lambda t} {m}}}$

куда v₀ - начальная скорость. Это означает, что скорость этой частицы распадается экспоненциально к нулю с течением времени. В этом случае эквивалентная точка зрения состоит в том, что кинетическая энергия частицы поглощается трением (которое преобразует ее в тепловую энергию в соответствии с сохранение энергии ), и частица замедляется. Это выражение может быть дополнительно проинтегрировано, чтобы получить положение р частицы как функция времени.

Важные силы включают сила гравитации и Сила Лоренца за электромагнетизм. Кроме того, Третий закон Ньютона иногда можно использовать для вывода сил, действующих на частицу: если известно, что частица А оказывает силу F на другой частице B, следует, что B должен проявлять равный и противоположный сила реакции, −F, на А. Сильная форма третьего закона Ньютона требует, чтобы F и -F действовать по линии, соединяющей А и B, а слабая форма - нет. Примеры слабой формы третьего закона Ньютона часто можно найти для магнитных сил.^{[требуется разъяснение ]}

Работа и энергия

Если постоянная сила F применяется к частице, которая совершает смещение Δр,^{[заметка 2]} то работа выполнена силой определяется как скалярное произведение векторов силы и смещения:

${displaystyle W = mathbf {F} cdot Delta mathbf {r},.}$

В более общем смысле, если сила изменяется в зависимости от положения, когда частица движется из р₁ к р₂ по пути C, работа, проделанная над частицей, задается линейный интеграл

${displaystyle W = int _ {C} mathbf {F} (mathbf {r}) cdot mathrm {d} mathbf {r},.}$

Если работа по перемещению частицы из р₁ к р₂ одинакова независимо от того, какой путь выбран, сила называется консервативный. Сила тяжести консервативная сила, как и сила идеализированного весна, как указано Закон Гука. Сила из-за трение неконсервативен.

В кинетическая энергия E_k частицы массы м путешествовать со скоростью v дан кем-то

${displaystyle E_ {mathrm {k}} = {frac {1} {2}} mv ^ {2} ,.}$

Для протяженных объектов, состоящих из многих частиц, кинетическая энергия составного тела является суммой кинетических энергий частиц.

В теорема работа – энергия утверждает, что для частицы постоянной массы м, общая работа W выполняется на частице, когда она движется из позиции р₁ к р₂ равно изменению кинетическая энергия E_k частицы:

${displaystyle W = Delta E_ {mathrm {k}} = E_ {mathrm {k_ {2}}} -E_ {mathrm {k_ {1}}} = {frac {1} {2}} mleft (v_ {2}) ^ {, 2} -v_ {1} ^ {, 2} ight) ,.}$

Консервативные силы можно выразить как градиент скалярной функции, известной как потенциальная энергия и обозначен E_п:

${displaystyle mathbf {F} = -mathbf {abla} E_ {mathrm {p}} ,.}$

Если все силы, действующие на частицу, консервативны, и E_п - полная потенциальная энергия (которая определяется как работа задействованных сил по изменению взаимного расположения тел), полученная путем суммирования потенциальных энергий, соответствующих каждой силе

${displaystyle mathbf {F} cdot Delta mathbf {r} = -mathbf {abla} E_ {mathrm {p}} cdot Delta mathbf {r} = -Delta E_ {mathrm {p}} ,.}$

Уменьшение потенциальной энергии равно увеличению кинетической энергии

${displaystyle -Delta E_ {mathrm {p}} = Delta E_ {mathrm {k}} Дельта правой стрелки (E_ {mathrm {k}} + E_ {mathrm {p}}) = 0 ,.}$

Этот результат известен как сохранение энергии и заявляет, что общая энергия,

${displaystyle sum E = E_ {mathrm {k}} + E_ {mathrm {p}} ,,}$

постоянна во времени. Это часто бывает полезно, потому что многие часто встречающиеся силы консервативны.

За пределами законов Ньютона

Классическая механика также описывает более сложные движения протяженных неточечных объектов. Законы Эйлера предоставить расширения к законам Ньютона в этой области. Концепции угловой момент полагаться на то же самое исчисление используется для описания одномерного движения. В уравнение ракеты расширяет понятие скорости изменения импульса объекта, чтобы включить в него эффекты «потери массы» объекта.

Есть две важные альтернативные формулировки классической механики: Лагранжева механика и Гамильтонова механика. Эти и другие современные формулировки обычно обходят понятие «сила», вместо этого ссылаясь на другие физические величины, такие как энергия, скорость и импульс, для описания механических систем в обобщенные координаты.

Приведенные выше выражения для импульса и кинетической энергии действительны только при отсутствии значительного электромагнитного вклада. В электромагнетизме второй закон Ньютона для токоведущих проводов нарушается, если не учитывать вклад электромагнитного поля в импульс системы, выраженный формулой Вектор Пойнтинга деленное на c², куда c это скорость света в свободном пространстве.

Пределы действия

Область применимости классической механики

Многие разделы классической механики представляют собой упрощения или приближения более точных форм; два самых точных существа общая теория относительности и релятивистский статистическая механика. Геометрическая оптика является приближением к квантовая теория света, и не имеет превосходной «классической» формы.

Когда и квантовая механика, и классическая механика неприменимы, например, на квантовом уровне со многими степенями свободы, квантовая теория поля (QFT) пригодится. QFT имеет дело с небольшими расстояниями и большими скоростями со многими степенями свободы, а также с возможностью любого изменения количества частиц во время взаимодействия. При рассмотрении больших степеней свободы на макроскопическом уровне статистическая механика становится полезным. Статистическая механика описывает поведение большого (но счетного) числа частиц и их взаимодействия в целом на макроскопическом уровне. Статистическая механика в основном используется в термодинамика для систем, выходящих за рамки предположений классической термодинамики. В случае высокого скорость объекты, приближающиеся к скорости света, классическая механика усиливается специальная теория относительности. В случае, если предметы становятся очень тяжелыми (т. Е. Их Радиус Шварцшильда не является пренебрежимо малым для данного приложения) отклонения от ньютоновской механики становятся очевидными и могут быть количественно определены с помощью Параметризованный постньютоновский формализм. В таком случае, Общая теория относительности (GR) становится применимым. Однако до сих пор нет теории Квантовая гравитация объединение ОТО и КТП в том смысле, что его можно использовать, когда объекты становятся очень маленькими и тяжелыми.[4] [5]

Ньютоновское приближение специальной теории относительности

В специальной теории относительности импульс частицы определяется выражением

${displaystyle mathbf {p} = {frac {mmathbf {v}} {sqrt {1- {frac {v ^ {2}} {c ^ {2}}}}}}} ,,}$

куда м - масса покоя частицы, v его скорость, v это модуль v, и c это скорость света.

Если v очень маленький по сравнению с c, v²/c² приблизительно равно нулю, поэтому

${displaystyle mathbf {p} приблизительно mmathbf {v},.}$

Таким образом, уравнение Ньютона п = мv представляет собой приближение релятивистского уравнения для тел, движущихся с малой скоростью по сравнению со скоростью света.

Например, релятивистская циклотронная частота циклотрон, гиротрон, или высокое напряжение магнетрон дан кем-то

${displaystyle f = f_ {mathrm {c}} {frac {m_ {0}} {m_ {0} + {frac {T} {c ^ {2}}}}} ,,}$

куда ж_c классическая частота электрона (или другой заряженной частицы) с кинетической энергией Т и (отдых ) масса м₀ кружить в магнитном поле. Масса (покоя) электрона 511 кэВ. Таким образом, частотная поправка составляет 1% для магнитной вакуумной трубки с ускоряющим напряжением постоянного тока 5,11 кВ.

Классическое приближение квантовой механики

Лучевое приближение классической механики нарушается, когда длина волны де Бройля не намного меньше других габаритов системы. Для нерелятивистских частиц эта длина волны равна

${displaystyle lambda = {frac {h} {p}}}$

куда час является Постоянная Планка и п это импульс.

Опять же, это происходит с электроны прежде, чем это произойдет с более тяжелыми частицами. Например, электроны, используемые Клинтон Дэвиссон и Лестер Гермер в 1927 году, ускоренный на 54 В, имел длину волны 0,167 нм, что было достаточно, чтобы показать один дифракция боковой лепесток при отражении от никеля кристалл с межатомным расстоянием 0,215 нм. С большим вакуумная камера, казалось бы, относительно легко увеличить угловое разрешение от радиана до миллирадиан и увидеть квантовую дифракцию от периодических структур Интегральная схема память компьютера.

Более практические примеры неудач классической механики в инженерном масштабе проводят квантовое туннелирование в туннельные диоды и очень узкий транзистор ворота в интегральные схемы.

Классическая механика такая же крайность высокочастотное приближение в качестве геометрическая оптика. Он более точен, потому что описывает частицы и тела с масса покоя. Они имеют больший импульс и, следовательно, более короткие длины волн Де Бройля, чем безмассовые частицы, такие как свет, с той же кинетической энергией.

История

Изучение движения тел - древнее, поэтому классическая механика стала одним из старейших и крупнейших предметов в мире. наука, инженерное дело и технологии.

Немного Греческие философы древности, среди них Аристотель, Основатель Аристотелевская физика, возможно, был первым, кто поддержал идею о том, что «все происходит по определенной причине» и что теоретические принципы могут помочь в понимании природы. В то время как для современного читателя многие из этих сохранившихся идей кажутся в высшей степени разумными, здесь явно не хватает математических теория и контролируемый эксперимент, как мы это знаем. Позже они стали решающими факторами в формировании современной науки, и их раннее применение стало известно как классическая механика.

В его Элемента супер демонстрация ponderum, средневековый математик Иорданус де Немор ввел понятие «позиционный сила тяжести "и использование компонента силы.

Три этапа Теория импульса в соответствии с Альберт Саксонский.

Первый опубликованный причинный объяснение движений планеты был Иоганн Кеплер Astronomia nova, опубликовано в 1609 году. Он сделал вывод, основываясь на Тихо Браге наблюдения на орбите Марс, что орбиты планеты были эллипсы. Этот разрыв с древняя мысль происходило примерно в то же время, что и Галилео предлагал абстрактные математические законы движения объектов. Возможно, он выполнил (а мог и не выполнил) знаменитый эксперимент по сбросу двух ядер разного веса с Пизанская башня, показывая, что они оба одновременно упали на землю. Реальность этого конкретного эксперимента оспаривается, но он действительно проводил количественные эксперименты, катая шары по наклонная плоскость. Его теория ускоренного движения была выведена на основе результатов таких экспериментов и составляет краеугольный камень классической механики.

сэр Исаак Ньютон (1643–1727), влиятельная фигура в истории физики, чья три закона движения составляют основу классической механики

Ньютон основал свои принципы естественной философии на трех предложенных законы движения: the закон инерции, его второй закон ускорения (упомянутый выше) и закон действие и реакция; и таким образом заложил основы классической механики. И второй, и третий законы Ньютона получили должное научное и математическое рассмотрение в теории Ньютона. Philosophiæ Naturalis Principia Mathematica. В этом их отличие от более ранних попыток объяснения подобных явлений, которые были либо неполными, либо неверными, либо имели мало точные математические выражения. Ньютон также провозгласил принципы сохранение импульса и угловой момент. В механике Ньютон также первым дал правильную научную и математическую формулировку сила тяжести в Закон всемирного тяготения Ньютона. Сочетание законов движения Ньютона и гравитации обеспечивает наиболее полное и точное описание классической механики. Он продемонстрировал, что эти законы применимы как к повседневным, так и к небесным объектам. В частности, он получил теоретическое объяснение Законы Кеплера движения планет.

Ньютон ранее изобрел исчисление, математики, и использовал его для выполнения математических вычислений. Для приемлемости, его книга, Principia, был сформулирован полностью в терминах давно установленных геометрических методов, которые вскоре были вытеснены его исчислением. Однако это было Лейбниц кто разработал обозначения производная и интеграл предпочтительный^[6] сегодня.

Гамильтон возможно, самый большой вклад - это переформулировка Ньютоновская механика, теперь называется Гамильтонова механика.

Ньютон и большинство его современников, за заметным исключением Гюйгенс, работал исходя из предположения, что классическая механика сможет объяснить все явления, включая свет, в виде геометрическая оптика. Даже при обнаружении так называемого Кольца Ньютона (а волновая интерференция феномен) он поддерживал собственное корпускулярная теория света.

После Ньютона классическая механика стала основной областью изучения математики, а также физики. Несколько переформулировок постепенно позволили найти решения гораздо большего числа проблем. Первая заметная переработка была сделана в 1788 г. Жозеф Луи Лагранж. В свою очередь, лагранжева механика была переформулирована в 1833 г. Уильям Роуэн Гамильтон.

Некоторые трудности были обнаружены в конце 19 века, которые могли быть разрешены только более современной физикой. Некоторые из этих трудностей связаны с совместимостью с электромагнитная теория, и знаменитый Эксперимент Майкельсона-Морли. Решение этих проблем привело к специальная теория относительности, часто до сих пор считается частью классической механики.

Вторая группа трудностей была связана с термодинамикой. В сочетании с термодинамика, классическая механика приводит к Парадокс гиббса классических статистическая механика, в котором энтропия не является точно определенной величиной. Излучение черного тела не было объяснено без введения кванты. Когда эксперименты достигли атомарного уровня, классическая механика не смогла объяснить даже приблизительно такие основные вещи, как уровни энергии и размеры атомы и фотоэлектрический эффект. Попытки решить эти проблемы привели к развитию квантовая механика.

С конца ХХ века классическая механика в физика больше не была независимой теорией. Вместо этого классическая механика теперь считается приближенной теорией к более общей квантовой механике. Акцент сместился на понимание фундаментальных сил природы, как в Стандартная модель и его более современные расширения в единую теория всего.^[7] Классическая механика - это теория, полезная для изучения движения неквантово-механических частиц с низкой энергией в слабых гравитационных полях. Кроме того, он был расширен на сложный домен где сложная классическая механика проявляет поведение, очень похожее на квантовую механику.^[8]

ветви

Классическая механика традиционно разделялась на три основных направления:

• Статика, изучение равновесие и его отношение к силы
• Динамика, изучение движения и его связи с силами
• Кинематика, имея дело с последствиями наблюдаемых движений, независимо от обстоятельств, их вызывающих.

Другое разделение основано на выборе математического формализма:

• Ньютоновская механика
• Лагранжева механика
• Гамильтонова механика

Как вариант, можно сделать разделение по регионам применения:

• Небесная механика, относящийся к звезды, планеты и другие небесные тела
• Механика сплошной среды, для материалов, моделируемых как континуум, например, твердые вещества и жидкости (т.е. жидкости и газы ).
• Релятивистская механика (т.е. включая специальный и Общее теории относительности), для тел, скорость которых близка к скорости света.
• Статистическая механика, который обеспечивает основу для связи микроскопических свойств отдельных атомов и молекул с макроскопическими или объемными термодинамический свойства материалов.

Смотрите также

Примечания

Рекомендации

дальнейшее чтение

• Алонсо, М .; Финн, Дж. (1992). Фундаментальная университетская физика. Эддисон-Уэсли.
• Фейнман, Ричард (1999). Лекции Фейнмана по физике. Издательство "Персей". ISBN  978-0-7382-0092-7.
• Фейнман, Ричард; Филлипс, Ричард (1998). Шесть легких пьес. Издательство "Персей". ISBN  978-0-201-32841-7.
• Гольдштейн, Герберт; Чарльз П. Пул; Джон Л. Сафко (2002). Классическая механика (3-е изд.). Эддисон Уэсли. ISBN  978-0-201-65702-9.
• Киббл, Том В.; Беркшир, Фрэнк Х. (2004). Классическая механика (5-е изд.). Imperial College Press. ISBN  978-1-86094-424-6.
• Клеппнер, Д .; Коленков, Р.Дж. (1973). Введение в механику. Макгроу-Хилл. ISBN  978-0-07-035048-9.
• Landau, L.D .; Лифшиц, Э.М. (1972). Курс теоретической физики, т. 1 - Механика. Книжная компания Франклина. ISBN  978-0-08-016739-8.
• Морен, Дэвид (2008). Введение в классическую механику: проблемы и решения (1-е изд.). Кембридж: Издательство Кембриджского университета. ISBN  978-0-521-87622-3.*Джеральд Джей Сассман; Джек Уиздом (2001). Структура и интерпретация классической механики. MIT Press. ISBN  978-0-262-19455-6.
• О'Доннелл, Питер Дж. (2015). Основная динамика и теория относительности. CRC Press. ISBN  978-1-4665-8839-4.
• Торнтон, Стивен Т .; Мэрион, Джерри Б. (2003). Классическая динамика частиц и систем (5-е изд.). Брукс Коул. ISBN  978-0-534-40896-1.

внешняя ссылка

• Кроуэлл, Бенджамин. Свет и материя (вводный текст, использует алгебру с дополнительными разделами, связанными с исчислением)
• Фитцпатрик, Ричард. Классическая механика (использует исчисление)
• Хойланд, Пол (2004). Предпочтительные системы отсчета и относительности
• Хорбач, Марко "Примечания к курсу классической механики ".
• Рошу, Харет К. "Классическая механика ". Физическое образование. 1999. [arxiv.org: Physics / 9909035]
• Шапиро, Джоэл А. (2003). Классическая механика
• Сассман, Джеральд Джей и мудрость, Джек и Майер, Мейнхард Э. (2001). Структура и интерпретация классической механики
• Тонг, Дэвид. Классическая динамика (Кембриджские конспекты лекций по лагранжиану и гамильтонову формализму)
• Кинематические модели для цифровой библиотеки дизайна (KMODDL)
  Фильмы и фотографии сотен работающих моделей механических систем на Корнелл Университет. Также включает библиотека электронных книг классических текстов по машиностроению и машиностроению.
• MIT OpenCourseWare 8.01: Классическая механика Бесплатные видеоролики актуальных лекций курса со ссылками на конспекты лекций, заданий и экзаменов.
• Алехандро А. Торасса, О классической механике