Генетический дрейф - Genetic drift

Часть серии по
Эволюционная биология
Зяблики Дарвина от Джон Гулд
Ключевые темы Введение в эволюцию Общий спуск Доказательства
Процессы и результаты Популяционная генетика Вариация Разнообразие Мутация Естественный отбор Приспособление Полиморфизм Генетический дрейф Генный поток Видообразование Адаптивное излучение Сотрудничество Коэволюция Соэкстинкция Расхождение Конвергенция Параллельная эволюция Вымирание
Естественная история Происхождение жизни История жизни Хронология эволюции Эволюция человека Филогения Биоразнообразие Биогеография Классификация Эволюционная таксономия Кладистика Переходное ископаемое Событие вымирания
История эволюционной теории Обзор эпоха Возрождения До Дарвина Дарвин Происхождение видов До синтеза Современный синтез Молекулярная эволюция Эво-дево Текущее исследование История видообразования История палеонтологии (Лента новостей )
Поля и приложения Приложения эволюции Биосоциальная криминология Экологическая генетика Эволюционная эстетика Эволюционная антропология Эволюционные вычисления Эволюционная экология Эволюционная экономика Эволюционная эпистемология Эволюционная этика Эволюционная теория игр Эволюционная лингвистика Эволюционная медицина Эволюционная нейробиология Эволюционная физиология Эволюционная психология Экспериментальная эволюция Филогенетика Палеонтология Селекция Видообразовательные эксперименты Социобиология Систематика Универсальный дарвинизм
Социальные последствия Эволюция как факт и теория Социальные эффекты Споры о сотворении и эволюции Возражения против эволюции Уровень поддержки
Портал эволюционной биологии  Категория похожие темы

Генетический дрейф (также известен как аллельный дрейф или Эффект Сьюолла Райта)^[1] изменение частоты существующих ген вариант (аллель ) в популяции из-за случайной выборки организмов.^[2] Аллели в потомстве являются выборкой аллелей у родителей, и шанс играет роль в определении того, выживет ли данный человек и будет ли он воспроизводиться. Население частота аллеля - это доля копий одного гена, имеющих определенную форму.^[3]

Генетический дрейф может привести к полному исчезновению вариантов генов и тем самым уменьшить генетическая вариация.^[4] Это также может привести к тому, что изначально редкие аллели стали намного более частыми и даже фиксированными.

Когда копий аллеля мало, влияние генетического дрейфа больше, а когда копий много, эффект меньше. В середине 20 века велись жаркие споры об относительной важности естественный отбор против нейтральных процессов, включая генетический дрейф. Рональд Фишер, который объяснил естественный отбор, используя Менделирующая генетика,^[5] придерживался мнения, что генетический дрейф играет в лучшем случае второстепенную роль в эволюция, и эта точка зрения оставалась доминирующей в течение нескольких десятилетий. В 1968 г. популяционный генетик Мотоо Кимура возобновил дебаты со своим нейтральная теория молекулярной эволюции, который утверждает, что в большинстве случаев генетические изменения распространяется по населению (хотя не обязательно меняется в фенотипы ) вызваны генетическим дрейфом, действующим на нейтральные мутации.^[6][7]

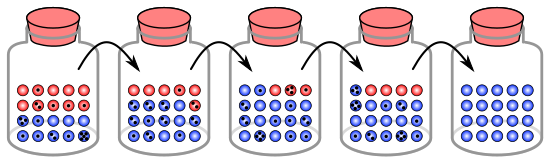
Аналогия с шариками в банке

Процесс генетического дрейфа можно проиллюстрировать с помощью 20 шариков в банке, представляющих 20 организмов в популяции.^[8] Считайте эту банку с шариками стартовой популяцией. Половина шариков в банке красная, а половина - синяя, причем каждый цвет соответствует разному аллелю одного гена в популяции. В каждом новом поколении организмы воспроизводятся случайным образом. Чтобы представить эту репродукцию, случайным образом выберите шарик из оригинальной банки и поместите новый шарик того же цвета в новую. Это «потомок» оригинального мрамора, то есть оригинальный мрамор остается в своей банке. Повторяйте этот процесс, пока во второй банке не будет 20 новых шариков. Во второй банке теперь будет 20 «потомков», или шариков разных цветов. Если во второй банке не содержится ровно 10 красных и 10 синих шариков, произошел случайный сдвиг частот аллелей.

Если этот процесс повторяется несколько раз, количество красных и синих шариков, собранных в каждом поколении, будет колебаться. Иногда в банке будет больше красных шариков, чем в «родительской» банке, а иногда больше синих. Это колебание аналогично генетическому дрейфу - изменению частоты аллелей в популяции в результате случайного изменения распределения аллелей от одного поколения к другому.

Возможно даже, что в каком-то одном поколении не будут выбраны шарики определенного цвета, что означает, что у них нет потомства. В этом примере, если красные шарики не выбраны, банка, представляющая новое поколение, содержит только голубые потомки. Если это произойдет, красный аллель будет навсегда потерян в популяции, а оставшийся синий аллель станет фиксированным: все будущие поколения будут полностью синими. В небольших популяциях фиксация может произойти всего за несколько поколений.

В этой симуляции каждая черная точка на шарике означает, что он был выбран для копирования (воспроизведения) один раз. Есть фиксация в синем «аллеле» в течение пяти поколений.

Вероятность и частота аллелей

Механизмы генетического дрейфа можно проиллюстрировать на упрощенном примере. Рассмотрим очень большую колонию бактерии изолирован в капле раствора. Бактерии генетически идентичны, за исключением одного гена с двумя помеченными аллелями. А и B. А и B являются нейтральными аллелями, что означает, что они не влияют на способность бактерий выживать и размножаться; все бактерии в этой колонии имеют равную вероятность выживания и размножения. Предположим, что половина бактерий имеет аллель А а другая половина имеет аллель B. Таким образом А и B каждый имеет частоту аллеля 1/2.

Затем капля раствора сжимается, пока в ней не останется пищи, достаточной для существования четырех бактерий. Все остальные бактерии погибают, не размножаясь. Среди четырех выживших шестнадцать возможных. комбинации для А и B аллели:

(А-А-А-А), (Б-А-А-А), (А-Б-А-А), (Б-Б-А-А),
(A-A-B-A), (B-A-B-A), (A-B-B-A), (B-B-B-A),
(A-A-A-B), (B-A-A-B), (A-B-A-B), (B-B-A-B),
(A-A-B-B), (B-A-B-B), (A-B-B-B), (B-B-B-B).

Поскольку все бактерии в исходном растворе с равной вероятностью выживут при сжатии раствора, четыре выживших представляют собой случайную выборку из исходной колонии. В вероятность то, что каждый из четырех выживших имеет данный аллель, составляет 1/2, и поэтому вероятность того, что любая конкретная комбинация аллелей произойдет, когда раствор сжимается,

${ displaystyle { frac {1} {2}} cdot { frac {1} {2}} cdot { frac {1} {2}} cdot { frac {1} {2}} = { frac {1} {16}}.}$

(Первоначальный размер популяции настолько велик, что выборка фактически происходит без замены). Другими словами, каждая из шестнадцати возможных комбинаций аллелей встречается с равной вероятностью с вероятностью 1/16.

Подсчет комбинаций с одинаковым количеством А и B, получаем следующую таблицу.

Как показано в таблице, общее количество комбинаций с одинаковым количеством А аллели по состоянию на B аллелей - шесть, а вероятность этой комбинации - 6/16. Общее количество других комбинаций равно десяти, поэтому вероятность неравного количества А и B аллелей - 10/16. Таким образом, хотя первоначальная колония началась с равным количеством А и B аллелей, вполне возможно, что количество аллелей в оставшейся популяции из четырех членов не будет равным. Равные числа на самом деле менее вероятны, чем неравные числа. В последнем случае произошел генетический дрейф, потому что частоты аллелей популяции изменились из-за случайной выборки. В этом примере популяция сократилась до четырех случайных выживших, явление, известное как узкое место населения.

Вероятности количества копий аллеля А (или B), которые выживают (данные в последнем столбце приведенной выше таблицы), можно рассчитать непосредственно из биномиальное распределение где вероятность «успеха» (вероятность присутствия данного аллеля) равна 1/2 (т.е. вероятность того, что есть k копии А (или B) аллели в комбинации) дается

${ displaystyle {n select k} left ({ frac {1} {2}} right) ^ {k} left (1 - { frac {1} {2}} right) ^ {nk } = {n choose k} left ({ frac {1} {2}} right) ^ {n} !}$

где п = 4 количество выживших бактерий.

Математические модели

Математические модели генетического дрейфа могут быть построены с использованием либо ветвящиеся процессы или уравнение диффузии описывающих изменения частоты аллелей в идеализированное население.^[9]

Модель Райта – Фишера

Рассмотрим ген с двумя аллелями, А или B. В диплоид население, состоящее из N лиц есть 2N копии каждого гена. У человека может быть две копии одного и того же аллеля или два разных аллеля. Мы можем назвать частоту одного аллеля п и частота других q. Модель Райта – Фишера (названа в честь Сьюэлл Райт и Рональд Фишер ) предполагает, что поколения не пересекаются (например, однолетние растения иметь ровно одно поколение в год) и что каждая копия гена, обнаруженная в новом поколении, отбирается независимо от всех копий гена в старом поколении. Формула для расчета вероятности получения k копии аллеля, который имел частоту п в последнем поколении тогда^[10][11]

${ displaystyle { frac {(2N)!} {k! (2N-k)!}} p ^ {k} q ^ {2N-k}}$

где символ "!"означает факториал функция. Это выражение также можно сформулировать с помощью биномиальный коэффициент,

${ displaystyle {2N choose k} p ^ {k} q ^ {2N-k}}$

Модель Морана

В Модель Морана предполагает перекрытие поколений. На каждом временном шаге выбирается одна особь для воспроизводства, а одна особь выбирается для смерти. Таким образом, на каждом временном шаге количество копий данного аллеля может увеличиваться на одну, уменьшаться на единицу или может оставаться неизменным. Это означает, что матрица перехода является трехдиагональный, что означает, что математические решения для модели Морана проще, чем для модели Райта – Фишера. С другой стороны, компьютерное моделирование обычно легче выполнять с использованием модели Райта – Фишера, потому что необходимо вычислять меньше временных шагов. В модели Морана требуется N временные шаги, чтобы пережить одно поколение, где N это эффективная численность населения. В модели Райта – Фишера требуется всего один.^[12]

На практике модели Морана и Райта – Фишера дают качественно аналогичные результаты, но генетический дрейф проходит в два раза быстрее в модели Морана.

Другие модели дрифта

Если дисперсия в количестве потомков намного больше, чем та, которую дает биномиальное распределение, предполагаемое моделью Райта-Фишера, то при той же общей скорости генетического дрейфа (эффективный размер дисперсии) дрейф генов является менее мощной силой по сравнению с выбором.^[13] Даже для такой же дисперсии, если она выше моменты Если распределение числа потомков превышает таковое при биномиальном распределении, то снова сила генетического дрейфа существенно ослабляется.^[14]

Случайные эффекты, отличные от ошибки выборки

Случайные изменения частот аллелей также могут быть вызваны другими эффектами, кроме ошибка выборки, например, случайные изменения давления отбора.^[15]

Один важный альтернативный источник стохастичность, возможно, важнее генетического дрейфа, генетический проект.^[16] Генетическая тяга - это влияние на локус путем выбора на связаны места. Математические свойства генетического проекта отличаются от свойств генетического дрейфа.^[17] Направление случайного изменения частоты аллелей: автокоррелированный через поколения.^[2]

Дрейф и фиксация

В Принцип Харди – Вайнберга утверждает, что в достаточно больших популяциях частоты аллелей остаются постоянными от одного поколения к другому, если равновесие не нарушается миграция, генетический мутации, или отбор.^[18]

Однако в конечных популяциях новые аллели не получаются из случайной выборки аллелей, переданных следующему поколению, но выборка может привести к исчезновению существующего аллеля. Потому что случайная выборка может удалять, но не заменять аллель, и поскольку случайное снижение или увеличение частоты аллелей влияет на ожидаемое распределение аллелей для следующего поколения, генетический дрейф ведет популяцию к генетической однородности с течением времени. Когда аллель достигает частоты 1 (100%), он считается «фиксированным» в популяции, а когда аллель достигает частоты 0 (0%), он теряется. Меньшие популяции достигают фиксации быстрее, тогда как в пределах бесконечной популяции фиксация не достигается. Как только аллель фиксируется, дрейф генов прекращается, и частота аллелей не может измениться, если в популяцию не будет введен новый аллель посредством мутации или поток генов. Таким образом, даже несмотря на то, что генетический дрейф является случайным, бесцельным процессом, он устраняет генетическая вариация через некоторое время.^[19]

Скорость изменения частоты аллелей из-за дрейфа

Десять симуляций случайного генетического дрейфа одного данного аллеля с начальным частотным распределением 0,5, измеренного в течение 50 поколений, повторенных в трех репродуктивно синхронных популяциях разного размера. В этих симуляциях аллели дрейфуют до потери или фиксации (частота 0,0 или 1,0) только в самой маленькой популяции.

Предполагая, что генетический дрейф - единственная эволюционная сила, действующая на аллель, после т поколений во многих реплицированных популяциях, начиная с частот аллелей п и q, дисперсия частоты аллелей в этих популяциях равна

${ displaystyle V_ {t} приблизительно pq left (1- exp left (- { frac {t} {2N_ {e}}} right) right)}$^[20]

Время фиксации или потери

Предполагая, что генетический дрейф является единственной эволюционной силой, действующей на аллель, в любой момент времени вероятность того, что аллель в конечном итоге закрепится в популяции, - это просто его частота в популяции в это время.^[21] Например, если частота п для аллеля А составляет 75%, а частота q для аллеля B составляет 25%, то при неограниченном времени вероятность А в конечном итоге закрепится в популяции, составляет 75%, и вероятность того, что B станет фиксированным - 25%.

Ожидаемое количество поколений для фиксации составляет пропорциональный зависит от размера популяции, так что фиксация, по прогнозам, будет происходить гораздо быстрее в небольших популяциях.^[22] Обычно для определения этих вероятностей используется эффективный размер популяции, который меньше, чем общая популяция. Эффективное население (N_е) учитывает такие факторы, как уровень инбридинг, стадия жизненного цикла, на которой популяция самая маленькая, и тот факт, что одни нейтральные гены генетически связаны с другими, находящимися в процессе отбора.^[13] Эффективный размер популяции не может быть одинаковым для каждого гена в одной и той же популяции.^[23]

Одна перспективная формула, используемая для аппроксимации ожидаемого времени до того, как нейтральный аллель станет фиксированным в результате генетического дрейфа, согласно модели Райта-Фишера:

${ displaystyle { bar {T}} _ { text {fixed}} = { frac {-4N_ {e} (1-p) ln (1-p)} {p}}}$

где Т это количество поколений, N_е - эффективный размер популяции, и п - начальная частота для данного аллеля. Результат - количество поколений ожидается пройти до того, как произойдет фиксация данного аллеля в популяции с заданным размером (N_е) и частоты аллелей (п).^[24]

Ожидаемое время потери нейтрального аллеля в результате генетического дрейфа можно рассчитать как^[10]

${ displaystyle { bar {T}} _ { text {lost}} = { frac {-4N_ {e} p} {1-p}} ln p.}$

Когда мутация появляется только один раз в популяции, достаточно большой для того, чтобы начальная частота была незначительной, формулы можно упростить до^[25]

${ displaystyle { bar {T}} _ { text {fixed}} = 4N_ {e}}$

для среднего числа поколений, ожидаемого до фиксации нейтральной мутации, и

${ displaystyle { bar {T}} _ { text {lost}} = 2 left ({ frac {N_ {e}} {N}} right) ln (2N)}$

для среднего числа поколений, ожидаемых до потери нейтральной мутации.^[26]

Время потерь с дрейфом и мутациями

Приведенные выше формулы применимы к аллелю, который уже присутствует в популяции и не подвержен ни мутации, ни естественному отбору. Если аллель теряется в результате мутации гораздо чаще, чем приобретается в результате мутации, то мутация, а также дрейф могут повлиять на время до потери. Если аллель, склонный к мутационной потере, начинается как фиксированный в популяции и теряется в результате мутации со скоростью m за репликацию, то ожидаемое время в поколениях до его потери в гаплоидной популяции определяется как

${ displaystyle { bar {T}} _ { text {lost}} приблизительно { begin {case} { dfrac {1} {m}}, { text {if}} mN_ {e} ll 1 [8pt] { dfrac { ln {(mN_ {e})} + gamma} {m}} { text {if}} mN_ {e} gg 1 end {case}}}$

где ${ displaystyle gamma}$ является Постоянная Эйлера.^[27] Первое приближение представляет собой время ожидания, пока первый мутант, обреченный на потерю, затем происходит относительно быстро из-за генетического дрейфа, требуя времени. N_е ≪ 1/м. Второе приближение представляет собой время, необходимое для детерминированной потери в результате накопления мутаций. В обоих случаях время до фиксации определяется мутацией через термин 1 /м, и меньше подвержен влиянию эффективная численность населения.

Против естественного отбора

В естественных популяциях генетический дрейф и естественный отбор не действуют изолированно; оба явления всегда присутствуют вместе с мутацией и миграцией. Нейтральная эволюция является продуктом мутации и дрейфа, а не только дрейфа. Точно так же, даже когда отбор преодолевает дрейф генов, он может воздействовать только на вариации, которые обеспечивает мутация.

Хотя у естественного отбора есть направление, ведущее эволюцию к наследуемому приспособления к текущей среде генетический дрейф не имеет направления и определяется только математика случая.^[28] В результате дрейф действует на генотипические частоты в популяции независимо от их фенотипических эффектов. Напротив, отбор способствует распространению аллелей, фенотипические эффекты которых увеличивают выживаемость и / или воспроизводство их носителей, снижает частоту аллелей, вызывающих неблагоприятные признаки, и игнорирует нейтральные.^[29]

В закон больших чисел предсказывает, что когда абсолютное количество копий аллеля невелико (например, в небольших группах населения ), величина дрейфа частот аллелей на поколение больше. Величина дрейфа достаточно велика, чтобы подавить отбор при любой частоте аллеля, когда коэффициент отбора меньше единицы, деленной на эффективный размер популяции. Неадаптивная эволюция, являющаяся результатом мутации и генетического дрейфа, поэтому считается последовательным механизмом эволюционных изменений, прежде всего в пределах небольших изолированных популяций.^[30] Математика генетического дрейфа зависит от эффективного размера популяции, но неясно, как это связано с фактическим количеством особей в популяции.^[16] Генетическая связь к другим генам, находящимся в процессе отбора, может уменьшить эффективный размер популяции нейтрального аллеля. С более высокой рекомбинация Скорость сцепления снижается, а вместе с тем и этот локальный эффект на эффективную численность населения.^[31][32] Этот эффект виден в молекулярных данных как корреляция между скоростью локальной рекомбинации и генетическое разнообразие,^[33] и отрицательная корреляция между плотностью генов и разнообразием на некодирующая ДНК регионы.^[34] Стохастичность, связанная со сцеплением с другими генами, находящимися в процессе отбора, не то же самое, что ошибка выборки, и иногда ее называют генетический проект чтобы отличить это от генетического дрейфа.^[16]

Когда частота аллелей очень мала, дрейф также может пересилить отбор даже в больших популяциях. Например, в то время как невыгодные мутации обычно быстро устраняются в больших популяциях, новые полезные мутации почти так же уязвимы для потери из-за генетического дрейфа, как и нейтральные мутации. До тех пор, пока частота аллеля полезной мутации не достигнет определенного порога, генетический дрейф не будет иметь никакого эффекта.^[29]

Узкое место среди населения

Изменения частоты аллелей в популяции после узкое место населения: быстрое и радикальное сокращение численности населения привело к сокращению численности населения генетическая вариация.

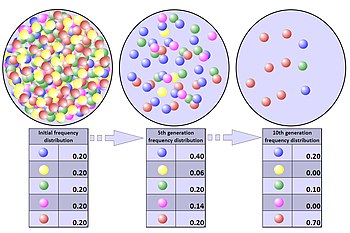
Узкое место популяции - это когда популяция сокращается до значительно меньших размеров за короткий период времени из-за какого-то случайного экологического события. В истинном «узком месте» популяции шансы на выживание любого члена популяции являются чисто случайными и не улучшаются каким-либо определенным генетическим преимуществом. Узкое место может привести к радикальным изменениям частот аллелей, совершенно независимо от отбора.^[35]

Воздействие узкого места в популяции может быть устойчивым, даже если оно вызвано разовым событием, таким как природная катастрофа. Интересным примером узкого места, вызывающего необычное генетическое распределение, является относительно высокая доля людей с общим числом стержневая ячейка дальтонизм (ахроматопсия ) на Атолл Пингелап в Микронезия. После узкого места инбридинг увеличивается. Это увеличивает ущерб, наносимый рецессивными вредными мутациями в процессе, известном как инбридинговая депрессия. Наихудшие из этих мутаций отбираются, что приводит к потере других аллелей, которые генетически связанный им, в процессе выбор фона.^[2] Для рецессивных вредных мутаций этот отбор может быть усилен как следствие узкого места из-за генетическая чистка. Это приводит к дальнейшей утрате генетического разнообразия. Кроме того, устойчивое сокращение размера популяции увеличивает вероятность дальнейших колебаний аллелей из-за дрейфа в грядущих поколениях.

Генетическая изменчивость популяции может быть значительно уменьшена из-за узкого места, и даже полезные адаптации могут быть навсегда устранены.^[36] Утрата изменчивости делает выжившую популяцию уязвимой для любого нового давления отбора, такого как болезни, изменение климата или сдвиг в доступном источнике пищи, потому что адаптация в ответ на изменения окружающей среды требует достаточного генетического разнообразия в популяции для естественного отбора.^[37][38]

В недавнем прошлом было много известных случаев нехватки населения. До приезда Европейцы, североамериканский прерии были средой обитания миллионов куры больших прерий. В Иллинойс только их численность упала с примерно 100 миллионов птиц в 1900 году до примерно 50 в 1990-х годах. Уменьшение численности популяции произошло в результате охоты и разрушения среды обитания, но следствием этого стала потеря большей части генетического разнообразия этого вида. ДНК Анализ сравнения птиц середины века с птицами 1990-х годов свидетельствует о резком снижении генетической изменчивости только за последние несколько десятилетий. В настоящее время цыпленок большой прерии испытывает низкий репродуктивный успех.^[39]

Однако генетическая потеря, вызванная узким местом и генетическим дрейфом, может повысить приспособленность, как в Эрлихия.^[40]

Чрезмерная охота также привела к серьезному ограничению численности населения в северный морской слон в 19 ​​веке. Их результирующее снижение генетической изменчивости можно вывести, сравнив его с уменьшением генетической изменчивости. южный морской слон, на которые не так агрессивно охотились.^[41]

Эффект основателя

Когда очень немногие члены популяции мигрируют, чтобы сформировать отдельную новую популяцию, возникает эффект основателя. В течение периода после основания небольшая популяция испытывает интенсивный дрейф. На рисунке это приводит к фиксации аллеля красного.

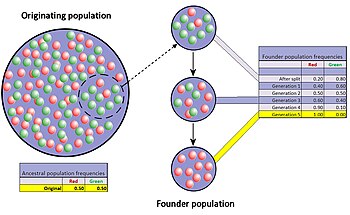
Эффект основателя - это особый случай узкого места популяции, возникающий, когда небольшая группа в популяции отделяется от первоначальной популяции и формирует новую. Ожидается, что случайная выборка аллелей в только что сформированной новой колонии сильно искажает исходную популяцию, по крайней мере, в некоторых отношениях.^[42] Возможно даже, что количество аллелей для некоторых генов в исходной популяции больше, чем количество копий генов в основателях, что делает невозможным полное представление. Когда новообразованная колония небольшая, ее основатели могут сильно повлиять на генетический состав популяции в далеком будущем.

Хорошо задокументированный пример можно найти в Амишей миграция в Пенсильвания в 1744 г. Два члена новой колонии разделяли рецессивный аллель Синдром Эллиса – ван Кревельда. Члены колонии и их потомки, как правило, религиозны изолированы и остаются относительно изолированными. В результате многих поколений инбридинга синдром Эллис-ван Кревельда в настоящее время гораздо более распространен среди амишей, чем среди населения в целом.^[29][43]

Разница в частотах генов между исходной популяцией и колонией также может вызвать у двух групп расходиться значительно на протяжении многих поколений. Как разница, или генетическая дистанция, увеличивается, две отдельные популяции могут стать разными, как генетически, так и фенетически, хотя этому расхождению способствуют не только генетический дрейф, но и естественный отбор, поток генов и мутации. Этот потенциал относительно быстрых изменений в частоте генов колонии побудил большинство ученых рассматривать эффект основателя (и, в более широком смысле, генетический дрейф) как значительную движущую силу в эволюции новые виды. Сьюэлл Райт был первым, кто придал такое значение случайному дрейфу и маленьким, недавно изолированным популяциям. теория смещения баланса видообразования.^[44] Следуя за Райтом, Эрнст Майр создали много убедительных моделей, чтобы показать, что снижение генетической изменчивости и небольшой размер популяции после эффекта основателя были критически важны для развития новых видов.^[45] Однако сегодня эта точка зрения пользуется гораздо меньшей поддержкой, поскольку гипотеза неоднократно проверялась экспериментальными исследованиями, и результаты были в лучшем случае неоднозначными.^[46]

История

Роль случайности в эволюции впервые была подчеркнута Арендом Л. Хагедорном и А. К. Хагедорном-Ворстхёвел ла Бранд Хагедорн в 1921 году.^[47] Они подчеркнули, что случайное выживание играет ключевую роль в потере разнообразия популяций. Фишер (1922) ответил на это первым, хотя и в некоторой степени неверным, математическим описанием «эффекта Хагедорна».^[48] Примечательно, что он ожидал, что многие естественные популяции были слишком большими (N ~ 10 000), чтобы эффекты дрейфа были существенными, и дрейф мысли имел незначительное влияние на эволюционный процесс. Исправленная математическая трактовка и термин «генетический дрейф» были позже введены в обращение основателем популяционная генетика, Сьюэлл Райт. Он впервые использовал термин «дрейф» в 1929 году.^[49] хотя в то время он использовал это в смысле направленного процесса изменения или естественного отбора. Случайный дрейф из-за ошибки выборки стал известен как «эффект Сьюолла – Райта», хотя ему никогда не было вполне комфортно, когда ему дали свое имя. Райт называл все изменения частоты аллелей либо «устойчивым дрейфом» (например, выбор), либо «случайным дрейфом» (например, ошибкой выборки).^[50] «Дрейф» стал использоваться как технический термин в стохастический смысл исключительно.^[51] Сегодня это обычно определяется еще более узко, с точки зрения ошибки выборки,^[52] хотя это узкое определение не универсально.^[53][54] Райт писал, что «ограничение« случайного дрейфа »или даже« дрейфа »только одним компонентом, последствия случайного отбора проб, как правило, приводит к путанице».^[50] Сьюэлл Райт рассматривал процесс случайного генетического дрейфа посредством ошибки выборки, эквивалентный таковому при инбридинге, но более поздние исследования показали, что они различны.^[55]

В первые дни современный эволюционный синтез, ученые начали смешивать новую науку о популяционной генетике с Чарльз Дарвин Российская теория естественного отбора. В рамках этой концепции Райт сосредоточился на влиянии инбридинга на небольшие относительно изолированные популяции. Он представил концепцию адаптивный ландшафт в которых такие явления, как скрещивание и генетический дрейф в небольших популяциях, могут оттолкнуть их от адаптивных пиков, что, в свою очередь, позволяет естественному отбору подтолкнуть их к новым адаптивным пикам.^[56] Райт считал, что более мелкие популяции больше подходят для естественного отбора, потому что «инбридинг был достаточно интенсивным, чтобы создать новые системы взаимодействия посредством случайного дрейфа, но недостаточно интенсивным, чтобы вызвать случайную неадаптивную фиксацию генов».^[57]

Взгляды Райта на роль генетического дрейфа в эволюционной схеме были противоречивыми почти с самого начала. Одним из самых громких и влиятельных критиков был коллега Рональд Фишер. Фишер признал, что генетический дрейф сыграл некоторую, но незначительную роль в эволюции. Фишера обвиняли в непонимании взглядов Райта, потому что в его критических замечаниях Фишер, казалось, утверждал, что Райт почти полностью отверг выбор. Для Фишера рассмотрение процесса эволюции как длительного, устойчивого и адаптивного развития было единственным способом объяснить постоянно растущую сложность более простых форм. Но споры между «градуалистами» и теми, кто больше склоняется к модели эволюции Райта, продолжаются, где отбор и дрейф вместе играют важную роль.^[58]

В 1968 г. Мотоо Кимура возродил дебаты своей нейтральной теорией молекулярной эволюции, которая утверждает, что большинство генетических изменений вызвано генетическим дрейфом, воздействующим на нейтральные мутации.^[6][7]

Роль генетического дрейфа посредством ошибки выборки в эволюции подвергалась критике со стороны Джон Х. Гиллеспи^[59] и Уильям Б. Провайн, которые утверждают, что отбор на связанных сайтах - более важная стохастическая сила.

Смотрите также

• Перипатрическое видообразование
• Антигенный дрейф
• Коалесцентная теория
• Генофонд
• Мейотический драйв

Примечания и ссылки

Список используемой литературы

внешние ссылки

• Шихи, Боб. «Программа моделирования популяционной генетики». Рэдфорд, Вирджиния: Рэдфордский университет. Получено 21 декабря 2015.
• Граймс, Билл. «Моделирование генетического дрейфа». Тусон, Аризона: Университет Аризоны. Получено 25 августа 2016.