Индусско-арабская система счисления - Hindu–Arabic numeral system
| Системы счисления |
|---|
| Индусско-арабская система счисления |
| Восточная Азия |
| Европейский |
| Американец |
| По алфавиту |
| Бывший |
| Позиционные системы к основание |
| Нестандартные позиционные системы счисления |
| Список систем счисления |

В Индусско-арабская система счисления или же Индо-арабская система счисления [1] (также называемый Арабская система счисления или же Индуистская система счисления)[2][примечание 1] это позиционный десятичный система счисления, и является наиболее распространенной системой символического представления чисел в мире.
Он был изобретен между I и IV веками Индийские математики. Система была принята в Арабская математика (также называемая исламской математикой) к 9 веку. Влиятельными были книги Аль-Хваризми[3] (О вычислении с помощью индусских цифр, c. 825) и Аль-Кинди (Об использовании индусских цифр, c. 830). Позднее эта система распространилась на средневековую Европу. Высокое средневековье.
Система основана на десяти (изначально девяти) глифы. Символы (глифы), используемые для представления системы, в принципе не зависят от самой системы. Фактически используемые глифы происходят от Цифры брахми и разделились на различные типографские варианты с момента Средний возраст.
Эти наборы символов можно разделить на три основных семейства: Западные арабские цифры используется в Великий Магриб И в Европа, Восточные арабские цифры (также называемые «индийскими цифрами»), используемые в Средний Восток, и индийские цифры в различных шрифтах, используемых в Индийский субконтинент.
Этимология
Индо-арабские или индо-арабские цифры были изобретены математиками в Индии.[4] Персидские и арабские математики называли их «индуистскими цифрами» (где «Индуистский «означает индийское»). Позже в Европе их стали называть «арабскими цифрами», потому что они были завезены на Запад арабскими купцами.[5]
Позиционное обозначение
Индусско-арабская система предназначена для позиционная запись в десятичный система. В более развитой форме позиционная запись также использует десятичный маркер (сначала знак над цифрой единиц, но теперь чаще десятичная точка или десятичная запятая, которая отделяет разряды единиц от разряда десятых), а также символ «эти цифры повторяются. до бесконечности ". В современном использовании этот последний символ обычно винкулум (горизонтальная черта над повторяющимися цифрами). В этой более развитой форме система счисления может символизировать любой Рациональное число используя только 13 символов (десять цифр, десятичный маркер, винкулум и добавленный знак минус указать отрицательное число ).
Хотя обычно встречается в текстах, написанных на арабском Абджад («алфавит») числа, написанные этими цифрами, также помещают наиболее значимую цифру слева, поэтому они читаются слева направо. Необходимые изменения направления чтения обнаруживаются в тексте, который сочетает в себе системы письма слева направо и системы письма справа налево.
Символы
Для представления чисел в индийско-арабской системе счисления используются различные наборы символов, большинство из которых были разработаны на основе Цифры брахми.
Символы, используемые для представления системы, разделились на различные типографские варианты, так как Средний возраст, разделенных на три основные группы:
- Широко распространенный западный "арабские цифры "используется с латинский, Кириллица, и Греческие алфавиты в таблице произошли от "западных арабских цифр", которые были разработаны в аль-Андалус и Магриб (есть два типографский стили для отображения западных арабских цифр, известных как фигуры накладки и текстовые рисунки ).
- «Арабский – Индийский» или «Восточные арабские цифры "используется с арабской графикой, разработанной в основном в современных Ирак.[нужна цитата ] Вариант восточных арабских цифр используется в персидском и урду.
- В Индийские цифры используется со сценариями Брахмическая семья в Индии и Юго-Восточной Азии. Каждый из примерно дюжины основных письменностей Индии имеет свои собственные числовые глифы (как можно заметить при просмотре таблиц символов Юникода).
Сравнение глифов
| # | Используется с алфавитами | Цифры | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | латинский, Кириллица, и Греческий | арабские цифры |
| 〇 / 零 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | Восточная Азия | Китайский, вьетнамский, Японский, и Корейские цифры |
| ο / ō | Αʹ | Βʹ | Γʹ | Δʹ | Εʹ | Ϛʹ | Ζʹ | Ηʹ | Θʹ | Современный греческий | Греческие цифры |
| א | ב | ג | ד | ה | ו | ז | ח | ט | иврит | Еврейские цифры | |
| ० | १ | २ | ३ | ४ | ५ | ६ | ७ | ८ | ९ | Деванагари | Числа деванагари |
| ૦ | ૧ | ૨ | ૩ | ૪ | ૫ | ૬ | ૭ | ૮ | ૯ | Гуджарати | Цифры гуджарати |
| ੦ | ੧ | ੨ | ੩ | ੪ | ੫ | ੬ | ੭ | ੮ | ੯ | Гурмукхи | Цифры гурмухи |
| ༠ | ༡ | ༢ | ༣ | ༤ | ༥ | ༦ | ༧ | ༨ | ༩ | тибетский | Тибетское письмо § Цифры |
| ০ | ১ | ২ | ৩ | ৪ | ৫ | ৬ | ৭ | ৮ | ৯ | Бенгальский / Ассамский | Бенгальские цифры |
| ೦ | ೧ | ೨ | ೩ | ೪ | ೫ | ೬ | ೭ | ೮ | ೯ | Каннада | Каннада скрипт § Цифры |
| ୦ | ୧ | ୨ | ୩ | ୪ | ୫ | ୬ | ୭ | ୮ | ୯ | Одиа | Цифры Одиа |
| ൦ | ൧ | ൨ | ൩ | ൪ | ൫ | ൬ | ൭ | ൮ | ൯ | Малаялам | Письмо малаялам § Другие символы |
| ௦ | ௧ | ௨ | ௩ | ௪ | ௫ | ௬ | ௭ | ௮ | ௯ | Тамильский | Тамильские цифры |
| ౦ | ౧ | ౨ | ౩ | ౪ | ౫ | ౬ | ౭ | ౮ | ౯ | телугу | Письмо телугу § Цифры |
| ០ | ១ | ២ | ៣ | ៤ | ៥ | ៦ | ៧ | ៨ | ៩ | Кхмерский | Кхмерские цифры |
| ๐ | ๑ | ๒ | ๓ | ๔ | ๕ | ๖ | ๗ | ๘ | ๙ | Тайский | Тайские цифры |
| ໐ | ໑ | ໒ | ໓ | ໔ | ໕ | ໖ | ໗ | ໘ | ໙ | Лаосский | Лаосский алфавит § Цифры |
| ၀ | ၁ | ၂ | ၃ | ၄ | ၅ | ၆ | ၇ | ၈ | ၉ | Бирманский | Бирманские цифры |
| ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ | ٨ | ٩ | арабский | Восточные арабские цифры |
| ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ | Персидский / Дари / Пушту | |
| ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ | Урду / Шахмухи | |
| ᠐ | ᠑ | ᠒ | ᠓ | ᠔ | ᠕ | ᠖ | ᠗ | ᠘ | ᠙ | Монгольский | Монгольские цифры |
История
Предшественники
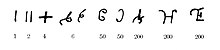
В Цифры брахми в основе системы до Наша эра. Они заменили более ранние Цифры Харости используется с 4 века до нашей эры. Числа Брахми и Хароши использовались рядом друг с другом в Империя Маурьев период, оба появились в 3 веке до н.э. указы Ашоки.[6]
Буддист в надписях примерно 300 г. до н.э. используются символы, которые стали 1, 4 и 6. Спустя столетие было зарегистрировано использование ими символов, которые стали 2, 4, 6, 7 и 9. Эти Цифры брахми являются предками индуистско-арабских знаков с 1 по 9, но они не использовались в качестве позиционная система с нуль, и для каждой десятки были отдельные цифры (10, 20, 30 и т. д.).
Фактическая система счисления, включая позиционное обозначение и использование нуля, в принципе не зависит от используемых глифов и значительно моложе, чем цифры Брахми.
Разработка

Система значений используется в Бахшалинская рукопись. Хотя дата составления рукописи неизвестна, язык, использованный в рукописи, указывает на то, что она не могла быть составлена позднее 400 г.[7] Развитие позиционной десятичной системы берет свое начало в Индуистская математика вовремя Период Гупта. Около 500 г. астроном Арьябхата использует слово ха («пустота») пометить «ноль» в табличном расположении цифр. 7 век Брахмаспхута Сиддханта содержит сравнительно глубокое понимание математической роли нуль. Санскритский перевод утраченного пракрита V века Джайнская космологическая текст Локавибхага может сохранить ранний пример позиционного использования нуля.[8]
Эти индийские разработки были рассмотрены в Исламская математика в 8 веке, как записано в аль-Кифти с Хронология ученых (начало 13 века).[9]
Система счисления стала известна как Персидский математик Хорезми кто написал книгу, О вычислении с помощью индусских цифр примерно в 825 г., а Араб математик Аль-Кинди кто написал книгу, Об использовании индусских цифр (كتاب في استعمال العداد الهندي [Китаб фи исти'мал аль-'адад аль-хинди]) около 830 г. Персидский ученый Кушьяр Гилани кто написал Китаб фи усул хисаб аль-хинд (Принципы индуистского исчисления ) - одна из старейших сохранившихся рукописей с использованием индусских цифр.[10] Эти книги несут основную ответственность за распространение индуистской системы счисления по всему миру. Исламский мир и в конечном итоге также в Европу.
Первая датированная и неоспоримая надпись, показывающая использование символа нуля, появляется на каменной надписи, найденной в Храм Чатурбхуджа в Гвалиор в Индии датируется 876 годом.[11]
В 10 веке Исламская математика, система была расширена за счет включения фракции, как записано в трактате Сирийский математик Абу'л-Хасан аль-Уклидиси в 952–953 гг.[12]
Усыновление в Европе

В христианской Европе первое упоминание и представление индусско-арабских цифр (от одного до девяти без нуля) находится в Кодекс Виджиланус, освещенный сборник различных исторических документов из Вестготский период в Испания, написанная в 976 году тремя монахами Риохан монастырь Сан-Мартин-де-Альбельда. Между 967 и 969 гг. Герберт из Орийака открыл и изучил арабскую науку в каталонских аббатствах. Позже он получил в этих местах книгу Умножение и деление (Об умножении и делении). Став Папа Сильвестр II в 999 году он представил новую модель счеты, так называемой Абак Герберта, приняв жетоны, представляющие индусско-арабские цифры от одного до девяти.
Леонардо Фибоначчи привез эту систему в Европу. Его книга Liber Abaci ввел арабские цифры, использование нуля и десятичную систему в латинский мир. Европейцы стали называть систему счисления «арабской». Он использовался в европейской математике с 12 века и вошел в широкое употребление с 15 века, чтобы заменить римские цифры.[13][14]
Знакомая форма западноарабских глифов, используемых в настоящее время в латинском алфавите (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), является продуктом конца 15 - начала 16 века, когда они войти рано наборный.Мусульманские ученые использовали Вавилонская система счисления, а продавцы использовали Цифры абджад, система, аналогичная Греческая система счисления и Ивритская система счисления. По аналогии, ФибоначчиВведение этой системы в Европу было ограничено кругами ученых. Заслуга за первое установление широкого понимания и использования десятичной позиционной записи среди населения в целом принадлежит Адам Райс, автор Немецкий ренессанс, чей 1522 г. Rechenung auff der linihen und federn был ориентирован на учеников бизнесменов и мастеров.

Грегор Райш, Мадам Арифматика, 1508

А таблица расчета, используется для арифметики с использованием римские цифры
Адам Райс, Rechenung auff der linihen und federn, 1522

Две книги по арифметике, изданные в 1514 году - Köbel (слева) с помощью расчетной таблицы и Böschenteyn используя цифры
Адам Райс, Rechenung auff der linihen und federn (2-е изд.), 1525 г.
Роберт Рекорд, Земля искусств, 1543
Питер Апиан, Kaufmanns Rechnung, 1527

Адам Райс, Rechenung auff der linihen und federn (2-е изд.), 1525 г.
Усыновление в Восточной Азии
В 690 г. н.э. Императрица Ву обнародованный Зетианские персонажи, одна из которых была "〇". Слово теперь используется как синоним числа ноль.
В Китай, Гаутама Сиддха ввел индусские цифры с нулем в 718, но Китайские математики не сочли их полезными, так как в них уже была десятичная позиционная счетные стержни.[15][16]
В китайских цифрах круг (〇) используется для записи нуля в Цифры Сучжоу. Многие историки считают, что он был импортирован из Индийские цифры к Гаутама Сиддха в 718 году, но некоторые китайские ученые считают, что он был создан из китайского текстового заполнителя пространства «□».[15]
Китайский и Японский наконец, в XIX веке были приняты индуистско-арабские цифры, отказавшись от счетных стержней.
Распространение западноарабского варианта

«Западные арабские» цифры, как они были широко использованы в Европе с Барокко период вторично нашли всемирное применение вместе с Латинский алфавит, и даже значительно превосходит современные распространение латинского алфавита, вторгаясь в системы письма в регионах, где использовались другие варианты индусско-арабских цифр, но также в сочетании с Китайский и Японский письмо (см. Китайские цифры, Японские цифры ).
Смотрите также
Примечания
- ^ Индуистский было персидским названием «индеец» в 10 веке, когда арабы приняли систему счисления. Использование "Индуистский «обращение к религии было более поздним развитием.
Рекомендации
- ^ Аудун Холме, Геометрия: наше культурное наследие, 2000
- ^ Уильям Даррах Холси, Эмануэль Фридман (1983). Энциклопедия Кольера с библиографией и указателем.
Когда арабская империя расширялась и был установлен контакт с Индией, индуистская система счисления и ранние алгоритмы были приняты арабами.
- ^ Брезина, Корона (2006), Аль-Хорезми: изобретатель алгебры, The Rosen Publishing Group, стр. 39–40, ISBN 978-1-4042-0513-0: «Историки высказывают предположения о родном языке аль-Хорезми. Поскольку он родился в бывшей персидской провинции, он, возможно, говорил на персидском языке. Также возможно, что он говорил на хорезмийском, языке региона, который сейчас вымер».
- ^ Кляйн, Феликс (2009). Элементарная математика с продвинутой точки зрения: арифметика, алгебра, анализ. Cosimo, Inc. ISBN 978-1605209319 - через Google Книги.
- ^ Роулетт, Расс (2004-07-04), Римские и "арабские" цифры, Университет Северной Каролины в Чапел-Хилл, получено 2019-04-12
- ^ Flegg (2002), стр. 6 и далее.
- ^ Пирс, Ян (май 2002 г.). «Бахшалинская рукопись». Архив истории математики MacTutor. Получено 2007-07-24.
- ^ Ифра, Г. Всеобщая история чисел: от предыстории до изобретения компьютера. John Wiley and Sons Inc., 2000. Перевод с французского Дэвида Беллоса, Э.Ф. Хардинга, Софи Вуд и Иана Монка.
- ^ аль-Кифти с Хронология ученых (начало 13 века):
- ... человек из Индии явился перед Халиф аль-Мансур в 776 году, который хорошо разбирался в методе расчета сиддханты, связанном с движением небесных тел, и имел способы вычисления уравнений, основанных на полухорде [по сути, синусе], вычисленной в полградусах ... Мансур приказал перевести эту книгу на арабский язык и написать на ее основе труд, чтобы дать арабам прочную основу для расчета движения планет ...
- ^ Мартин Леви и Марвин Петрук, Принципы индуистского исчисления, перевод Кушьяра ибн Лаббана Китаба фи усул хисаб аль-хинд, стр. 3, University of Wisconsin Press, 1965 г.
- ^ Билл Кассельман (Февраль 2007 г.). "Все напрасно". Столбец функций. AMS.
- ^ Берггрен, Дж. Леннарт (2007). «Математика в средневековом исламе». Математика Египта, Месопотамии, Китая, Индии и ислама: Справочник. Издательство Принстонского университета. п. 518. ISBN 978-0-691-11485-9.
- ^ «Числа Фибоначчи». www.halexandria.org.
- ^ Леонардо Пизано: «Вклад в теорию чисел». Британская энциклопедия Online, 2006. с. 3. Проверено 18 сентября 2006 г.
- ^ а б Цянь, Баоцун (1964), Чжунго Шусюэ Ши (История китайской математики), Пекин: Кэсюэ Чубанше
- ^ Ван, Qīngxiáng (1999), Санги о коэта отоко (Человек, который превзошел количество счетных стержней), Токио: Тёё Сётэн, ISBN 4-88595-226-3
Библиография
- Флегг, Грэм (2002). Числа: их история и значение. Courier Dover Publications. ISBN 0-486-42165-1.
- Арабская система счисления - MacTutor History of Mathematics
дальнейшее чтение
- Меннингер, Карл В. (1969). Числовые слова и цифровые символы: культурная история чисел. MIT Press. ISBN 0-262-13040-8.
- Эдвард Клайв Бейли о генеалогии современных цифр








