Временные ряды - Time series

Временные ряды: случайные данные плюс тренд, с наиболее подходящей линией и различными примененными фильтрами

А Временные ряды это серия точки данных проиндексированы (или занесены в список или графически отображены) по времени. Чаще всего временной ряд представляет собой последовательность взятые в последовательные равноотстоящие моменты времени. Таким образом, это последовательность дискретное время данные. Анализ временных рядов может быть полезен, чтобы увидеть, как данный актив, ценная бумага или экономическая переменная изменяется с течением времени. Примеры временных рядов - высоты океана. приливы, количество солнечные пятна, и дневная стоимость закрытия Промышленный индекс Доу-Джонса.

Временные ряды очень часто строятся с помощью запускать графики (временный линейный график ). Временные ряды используются в статистика, обработка сигналов, распознавание образов, эконометрика, математические финансы, прогноз погоды, прогноз землетрясения, электроэнцефалография, техника управления, астрономия, коммуникационная техника, и во многом в любой области прикладной наука и инженерное дело который включает временный измерения.

Временные ряды анализ содержит методы анализа данных временных рядов с целью извлечения значимой статистики и других характеристик данных. Временные ряды прогнозирование это использование модель для прогнозирования будущих значений на основе ранее наблюдаемых значений. Пока регрессивный анализ часто используется для проверки теорий о том, что текущие значения одного или нескольких независимых временных рядов влияют на текущее значение другого временного ряда, этот тип анализа временных рядов не называется «анализом временных рядов», который фокусируется на сравнение значений одного временного ряда или нескольких зависимых временных рядов в разные моменты времени. Прерванный временной ряд Анализ - это анализ вмешательств на одном временном ряду.

Данные временных рядов имеют естественный временной порядок. Это отличает анализ временных рядов от поперечные исследования, в котором нет естественного упорядочивания наблюдений (например, объяснение заработной платы людей со ссылкой на их соответствующий уровень образования, где данные отдельных лиц можно вводить в любом порядке). Анализ временных рядов также отличается от анализ пространственных данных где наблюдения обычно относятся к географическому местоположению (например, учет цен на жилье по местоположению, а также внутренним характеристикам домов). А стохастический Модель для временного ряда обычно будет отражать тот факт, что близкие по времени наблюдения будут более тесно связаны, чем более удаленные друг от друга. Кроме того, модели временных рядов часто используют естественное одностороннее упорядочение времени, так что значения для данного периода будут выражаться как производные некоторым образом из прошлых значений, а не из будущих значений (см. обратимость времени.)

Анализ временных рядов может применяться к ценный, непрерывные данные, дискретный числовой данные или дискретные символьные данные (то есть последовательности символов, такие как буквы и слова в английский язык[1]).

Методы анализа

Методы анализа временных рядов можно разделить на два класса: частотная область методы и область времени методы. К первым относятся спектральный анализ и вейвлет-анализ; последние включают автокорреляция и взаимная корреляция анализ. Во временной области корреляция и анализ могут выполняться аналогично фильтру с использованием масштабированная корреляция, тем самым уменьшая необходимость работы в частотной области.

Кроме того, методы анализа временных рядов можно разделить на параметрический и непараметрический методы. В параметрические подходы предполагаем, что основной стационарный случайный процесс имеет определенную структуру, которую можно описать с помощью небольшого количества параметров (например, с помощью авторегрессия или же модель скользящего среднего ). В этих подходах задача состоит в оценке параметров модели, описывающей случайный процесс. Напротив, непараметрические подходы явно оценить ковариация или спектр процесса, не предполагая, что процесс имеет какую-либо конкретную структуру.

Методы анализа временных рядов также можно разделить на линейный и нелинейный, и одномерный и многомерный.

Данные панели

Временной ряд - это один из видов данные панели. Панельные данные - это общий класс, многомерный набор данных, тогда как набор данных временных рядов - это одномерная панель (как и набор данных поперечного сечения ). Набор данных может демонстрировать характеристики как панельных данных, так и данных временных рядов. Один из способов узнать - спросить, что отличает одну запись данных от других. Если ответом является поле временных данных, то это кандидат на набор данных временного ряда. Если для определения уникальной записи требуется поле данных о времени и дополнительный идентификатор, не связанный со временем (идентификатор студента, символ акций, код страны), то это кандидат на данные панели. Если различие заключается в не-временном идентификаторе, тогда набор данных является кандидатом на набор перекрестных данных.

Анализ

Существует несколько типов мотивации и анализа данных, доступных для временных рядов, которые подходят для разных целей.

Мотивация

В контексте статистика, эконометрика, количественное финансирование, сейсмология, метеорология, и геофизика Основная цель анализа временных рядов - прогнозирование. В контексте обработка сигналов, техника управления и коммуникационная техника он используется для обнаружения сигналов и оценка.[нужна цитата ] В контексте сбор данных, распознавание образов и машинное обучение анализ временных рядов может использоваться для кластеризация,[2][3] классификация,[4] запрос по содержанию,[5] обнаружение аномалии а также прогнозирование.[нужна цитата ]

Исследовательский анализ

Заболеваемость туберкулезом США 1953-2009 гг.
Дальнейшая информация: Исследовательский анализ

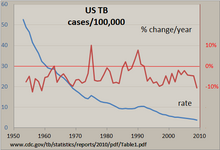
Самый простой способ изучить обычный временной ряд вручную - это линейный график например, показанный для туберкулеза в Соединенных Штатах, сделанный с помощью программы электронных таблиц. Количество случаев было стандартизовано по ставке на 100 000 и рассчитано процентное изменение этой ставки за год. Линия, которая почти неуклонно опускается, показывает, что заболеваемость туберкулезом снижалась на протяжении многих лет, но процентное изменение этого показателя варьировалось на целых +/- 10% с «всплесками» в 1975 году и примерно в начале 1990-х годов. Использование обеих вертикальных осей позволяет сравнивать два временных ряда на одном графике.

Другие техники включают:

Подгонка кривой

Основная статья: Подгонка кривой

Подгонка кривой[8][9] это процесс построения изгиб, или же математическая функция, который лучше всего подходит для серии данные точки,[10] возможно при наличии ограничений.[11][12] Аппроксимация кривой может включать либо интерполяция,[13][14] где требуется точное соответствие данным, или сглаживание,[15][16] в котором построена "гладкая" функция, которая приблизительно соответствует данным. Связанная тема регрессивный анализ,[17][18] который больше фокусируется на вопросах статистические выводы например, сколько неопределенности присутствует в кривой, которая соответствует данным, наблюдаемым со случайными ошибками. Подгоняемые кривые можно использовать как вспомогательные средства для визуализации данных,[19][20] чтобы вывести значения функции при отсутствии данных,[21] и резюмировать отношения между двумя или более переменными.[22] Экстраполяция относится к использованию подобранной кривой за пределами классифицировать наблюдаемых данных,[23] и подлежит степень неопределенности[24] поскольку он может отражать метод, использованный для построения кривой, в той же степени, в какой он отражает наблюдаемые данные.

Построение экономических временных рядов включает оценку некоторых компонентов для некоторых дат с помощью интерполяция между значениями («контрольными отметками») для более ранней и более поздней даты. Интерполяция - это оценка неизвестной величины между двумя известными величинами (исторические данные) или вывод об отсутствующей информации из доступной информации («чтение между строк»).[25] Интерполяция полезна, когда данные, окружающие недостающие данные, доступны и известны их тенденции, сезонность и долгосрочные циклы. Это часто делается с использованием связанных рядов, известных на все соответствующие даты.[26] Альтернативно полиномиальная интерполяция или же сплайн-интерполяция используется там, где кусочно многочлен функции вписываются во временные интервалы, так что они плавно сочетаются друг с другом. Другая проблема, которая тесно связана с интерполяцией, - это приближение сложной функции простой функцией (также называемой регресс Основное различие между регрессией и интерполяцией заключается в том, что полиномиальная регрессия дает один полином, который моделирует весь набор данных. Однако сплайн-интерполяция дает кусочно-непрерывную функцию, состоящую из множества многочленов для моделирования набора данных.

Экстраполяция - это процесс оценки значения переменной за пределами исходного диапазона наблюдения на основе ее взаимосвязи с другой переменной. Это похоже на интерполяция, который дает оценки между известными наблюдениями, но экстраполяция требует большего неуверенность и более высокий риск получения бессмысленных результатов.

Аппроксимация функции

Основная статья: Аппроксимация функции

В общем, задача аппроксимации функции требует от нас выбора функция среди четко определенного класса, который близко соответствует («приближает») целевой функции в зависимости от конкретной задачи. Можно выделить два основных класса задач аппроксимации функций: во-первых, для известных целевых функций теория приближения это филиал числовой анализ который исследует, как определенные известные функции (например, специальные функции ) могут быть аппроксимированы определенным классом функций (например, многочлены или же рациональные функции ), которые часто имеют желаемые свойства (недорогие вычисления, непрерывность, интегральные и предельные значения и т. д.).

Во-вторых, целевая функция, назовите ее грамм, может быть неизвестно; вместо явной формулы, только набор точек (временной ряд) вида (Икс, грамм(Икс)) предоставлен. В зависимости от структуры домен и codomain из грамм, несколько методов аппроксимации грамм может быть применимо. Например, если грамм это операция на действительные числа, техники интерполяция, экстраполяция, регрессивный анализ, и подгонка кривой может быть использован. Если codomain (диапазон или целевой набор) из грамм конечное множество, мы имеем дело с классификация проблема вместо этого. Связанная проблема онлайн приближение временного ряда[27] заключается в суммировании данных за один проход и построении приблизительного представления, которое может поддерживать различные запросы временных рядов с пределами наихудшей ошибки.

В какой-то степени разные проблемы (регресс, классификация, приближение пригодности ) получили единый режим в теория статистического обучения, где они рассматриваются как контролируемое обучение проблемы.

Прогнозирование и прогнозирование

В статистика, прогноз является частью статистические выводы. Один из конкретных подходов к такому выводу известен как предсказательный вывод, но прогноз может быть выполнен в рамках любого из нескольких подходов к статистическому выводу. Действительно, одно из описаний статистики заключается в том, что она обеспечивает средство передачи знаний об выборке совокупности всему населению и другим связанным популяциям, что не обязательно совпадает с прогнозированием во времени. Когда информация передается во времени, часто в определенные моменты времени, этот процесс известен как прогнозирование.

  • Полностью сформированные статистические модели для стохастическое моделирование целей, чтобы создать альтернативные версии временных рядов, представляющие, что может произойти в неопределенные периоды времени в будущем.
  • Простые или полностью сформированные статистические модели для описания вероятного результата временного ряда в ближайшем будущем с учетом информации о самых последних результатах (прогнозирование).
  • Прогнозирование временных рядов обычно выполняется с использованием пакетов автоматизированного статистического программного обеспечения и языков программирования, таких как Юля, Python, р, SAS, SPSS и много других.
  • Прогнозирование крупномасштабных данных выполняется с помощью Spark, который имеет Spark-ts в качестве стороннего пакета.

Классификация

Основная статья: Статистическая классификация

Присвоение шаблона временного ряда к определенной категории, например, определение слова на основе серии движений руки в язык знаков.

Оценка сигнала

Смотрите также: Обработка сигналов и Теория оценок

Этот подход основан на гармонический анализ и фильтрация сигналов в частотная область с использованием преобразование Фурье, и оценка спектральной плотности, развитие которых значительно ускорилось в Вторая Мировая Война математиком Норберт Винер, инженеры-электрики Рудольф Э. Кальман, Деннис Габор и другие для фильтрации сигналов от шума и прогнозирования значений сигналов в определенный момент времени. Видеть Фильтр Калмана, Теория оценок, и Цифровая обработка сигналов

Сегментация

Основная статья: Сегментация временных рядов

Разделение временного ряда на последовательность сегментов. Часто временной ряд может быть представлен как последовательность отдельных сегментов, каждый из которых имеет свои характерные свойства. Например, аудиосигнал конференц-связи можно разделить на части, соответствующие времени, в течение которого говорил каждый человек. При сегментации временных рядов цель состоит в том, чтобы идентифицировать граничные точки сегмента во временном ряду и охарактеризовать динамические свойства, связанные с каждым сегментом. К этой проблеме можно подойти, используя обнаружение точки изменения или путем моделирования временных рядов как более сложной системы, такой как линейная система марковских скачков.

Модели

Модели для данных временных рядов могут иметь множество форм и представлять разные случайные процессы. При моделировании вариаций уровня процесса три основных класса практического значения: авторегрессия (AR) модели интегрированный (I) модели, а скользящая средняя (MA) модели. Эти три класса линейно зависят от предыдущих точек данных.[28] Комбинации этих идей создают авторегрессионная скользящая средняя (ARMA) и авторегрессионная интегрированная скользящая средняя (ARIMA) модели. В авторегрессионное дробно-интегрированное скользящее среднее (ARFIMA) модель обобщает первые три. Расширения этих классов для работы с векторными данными доступны под заголовком многомерных моделей временных рядов, а иногда предшествующие аббревиатуры расширяются за счет включения начальной буквы «V» для «вектора», как в VAR для векторная авторегрессия. Дополнительный набор расширений этих моделей доступен для использования в тех случаях, когда наблюдаемые временные ряды управляются некоторыми «принудительными» временными рядами (которые могут не иметь причинного воздействия на наблюдаемые ряды): отличие от многомерного случая в том, что серия принуждения может быть детерминированной или находиться под контролем экспериментатора. Для этих моделей аббревиатуры дополняются финальной буквой «X», означающей «экзогенный».

Нелинейная зависимость уровня ряда от предыдущих точек данных представляет интерес, отчасти из-за возможности получения хаотичный Временные ряды. Однако, что более важно, эмпирические исследования могут указать на преимущество использования прогнозов, полученных на основе нелинейных моделей, по сравнению с прогнозами на основе линейных моделей, как, например, в нелинейные авторегрессионные экзогенные модели. Дополнительные ссылки на нелинейный анализ временных рядов: (Kantz and Schreiber),[29] и (Абарбанель)[30]

Среди других типов моделей нелинейных временных рядов есть модели для представления изменений дисперсии во времени (гетероскедастичность ). Эти модели представляют авторегрессионная условная гетероскедастичность (ARCH) и коллекция включает в себя самые разные представления (ГАРЧ, TARCH, EGARCH, FIGARCH, CGARCH и т. Д.). Здесь изменения изменчивости связаны с недавними прошлыми значениями наблюдаемых рядов или предсказываются ими. Это контрастирует с другими возможными представлениями локально изменяющейся изменчивости, где изменчивость может быть смоделирована как управляемая отдельным изменяющимся во времени процессом, как в дважды стохастическая модель.

В недавних работах по безмодельному анализу методы, основанные на вейвлет-преобразовании (например, локальные стационарные вейвлеты и нейронные сети, разложенные по вейвлетам), получили признание. Методы многоуровневого (часто называемого множественным разрешением) разлагают данный временной ряд, пытаясь проиллюстрировать временную зависимость в нескольких масштабах. Смотрите также Марковский переключающий мультифрактал (MSMF) методы моделирования эволюции волатильности.

А Скрытая марковская модель (HMM) - это статистическая марковская модель, в которой моделируемая система считается марковским процессом с ненаблюдаемыми (скрытыми) состояниями. HMM можно рассматривать как простейший динамическая байесовская сеть. Модели HMM широко используются в распознавание речи, для перевода временного ряда произнесенных слов в текст.

Обозначение

Для анализа временных рядов используется ряд различных обозначений. Обычное обозначение, определяющее временной ряд Икс который индексируется натуральные числа написано

Икс = {Икс1, Икс2, ...}.

Еще одно распространенное обозначение:

Y = {Yт: т ∈ Т},

куда Т это набор индексов.

Условия

Есть два набора условий, при которых строится большая часть теории:

Однако идеи стационарности необходимо расширить, чтобы учесть две важные идеи: строгая стационарность и стационарность второго порядка. И модели, и приложения могут быть разработаны при каждом из этих условий, хотя модели в последнем случае можно рассматривать как частично определенные.

Кроме того, анализ временных рядов может применяться, когда ряды сезонный стационарный или нестационарный. Ситуации, когда амплитуды частотных составляющих меняются со временем, можно разрешить в частотно-временной анализ который использует частотно-временное представление временного ряда или сигнала.[31]

Инструменты

Инструменты для исследования данных временных рядов включают:

Меры

Метрики временных рядов или Особенности который можно использовать для временных рядов классификация или же регрессивный анализ:[35]

Визуализация

Временные ряды можно визуализировать с помощью двух категорий диаграмм: перекрывающихся диаграмм и отдельных диаграмм. Перекрывающиеся диаграммы отображают все временные ряды в одном макете, в то время как отдельные диаграммы представляют их в разных макетах (но выровнены для целей сравнения)[39]

Перекрывающиеся графики

Отдельные диаграммы

  • Графики горизонта
  • Уменьшенная линейная диаграмма (малые кратные)
  • График силуэта
  • Круговой силуэт графика

Смотрите также

Рекомендации

  1. ^ Лин, Джессика; Кио, Имонн; Лонарди, Стефано; Чиу, Билл (2003). «Символическое представление временных рядов с последствиями для алгоритмов потоковой передачи». Материалы 8-го семинара ACM SIGMOD по вопросам исследований в области интеллектуального анализа данных и открытия знаний. Нью-Йорк: ACM Press. С. 2–11. CiteSeerX  10.1.1.14.5597. Дои:10.1145/882082.882086. S2CID  6084733.
  2. ^ Ляо, Т. Уоррен (2005). «Кластеризация данных временных рядов - обзор». Распознавание образов. Эльзевир. 38 (11): 1857–1874. Дои:10.1016 / j.patcog.2005.01.025. - через ScienceDirect (требуется подписка)
  3. ^ Агабозорги, Саид; Ширхоршиди, Али С .; Вах, Тех Ю. (2015). «Кластеризация временных рядов - обзор десятилетия». Информационные системы. Эльзевир. 53: 16–38. Дои:10.1016 / j.is.2015.04.007. - через ScienceDirect (требуется подписка)
  4. ^ Кио, Имонн Дж. (2003). «О необходимости тестов для интеллектуального анализа данных временных рядов». Интеллектуальный анализ данных и обнаружение знаний. Kluwer. 7: 349–371. Дои:10.1145/775047.775062. ISBN  158113567X. - через ACM Digital Library (требуется подписка)
  5. ^ Агравал, Ракеш; Фалаутсос, Христос; Свами, Арун (октябрь 1993 г.). «Эффективный поиск сходства в базах данных последовательностей». Материалы 4-й Международной конференции по основам организации данных и алгоритмов. Международная конференция по основам организации данных и алгоритмов. 730. С. 69–84. Дои:10.1007/3-540-57301-1_5. - через SpringerLink (требуется подписка)
  6. ^ Блумфилд, П. (1976). Фурье-анализ временных рядов: введение. Нью-Йорк: Вили. ISBN  978-0471082569.
  7. ^ Шамуэй, Р. Х. (1988). Прикладной статистический анализ временных рядов. Энглвуд Клиффс, Нью-Джерси: Prentice Hall. ISBN  978-0130415004.
  8. ^ Сандра Лах Арлингхаус, PHB Практическое руководство по аппроксимации кривой. CRC Press, 1994.
  9. ^ Уильям М. Колб. Подгонка кривой для программируемых калькуляторов. Syntec, Incorporated, 1984 г.
  10. ^ С.С. Халли, К.В. Рао. 1992. Передовые методы анализа населения. ISBN  0306439972 Стр.165 (ср. ... функции выполняются, если у нас есть хорошее или умеренное соответствие наблюдаемым данным.)
  11. ^ Сигнал и шум: Почему так много прогнозов не оправдываются, а некоторые - нет. Автор Нейт Сильвер
  12. ^ Подготовка данных для интеллектуального анализа данных: Текст. Автор Дориан Пайл.
  13. ^ Численные методы в инженерии с MATLAB®. К Яан Киусалаас. Стр.24.
  14. ^ Численные методы в разработке с Python 3. Автор Яан Киусалаас. Стр.21.
  15. ^ Численные методы аппроксимации кривой. Авторы: П. Г. Гест, Филипп Джордж Гест. Стр. 349.
  16. ^ Смотрите также: Успокаивающий
  17. ^ Подбор моделей к биологическим данным с помощью линейной и нелинейной регрессии. Харви Мотульски, Артур Христопулос.
  18. ^ Регрессионный анализ Рудольф Дж. Фройнд, Уильям Дж. Уилсон, Ping Sa. Стр. 269.
  19. ^ Визуальная информатика. Под редакцией Халимы Бадиозе Заман, Питера Робинсона, Марии Петру, Патрика Оливье, Хайко Шредера. Стр. 689.
  20. ^ Численные методы для нелинейных инженерных моделей. Джон Р. Хаузер. Стр. 227.
  21. ^ Методы экспериментальной физики: спектроскопия, том 13, часть 1. Клэр Мартон. Стр.150.
  22. ^ Энциклопедия дизайна исследования, том 1. Под редакцией Нила Дж. Салкинда. Стр. 266.
  23. ^ Методы анализа и планирования сообщества. Ричард Э. Клостерман. Страница 1.
  24. ^ Введение в риск и неопределенность в оценке экологических инвестиций. Издательство ДИАНА. Стр. 69
  25. ^ Хэмминг, Ричард. Численные методы для ученых и инженеров. Курьерская корпорация, 2012 г.
  26. ^ Фридман, Милтон. "Интерполяция временных рядов по связанным рядам. »Журнал Американской статистической ассоциации 57.300 (1962): 729–757.
  27. ^ Ганди, Сораб, Лука Фошини и Субхаш Сури. "Экономичная онлайн-аппроксимация данных временных рядов: потоки, амнезия и нарушение порядка. »Data Engineering (ICDE), 26-я Международная конференция IEEE, 2010 г., IEEE, 2010.
  28. ^ Гершенфельд, Н. (1999). Природа математического моделирования. Нью-Йорк: Издательство Кембриджского университета. стр.205 –208. ISBN  978-0521570954.
  29. ^ Канц, Хольгер; Томас, Шрайбер (2004). Нелинейный анализ временных рядов. Лондон: Издательство Кембриджского университета. ISBN  978-0521529020.
  30. ^ Абарбанель, Генри (25 ноября 1997 г.). Анализ наблюдаемых хаотических данных. Нью-Йорк: Спрингер. ISBN  978-0387983721.
  31. ^ Боашаш, Б. (ред.), (2003) Частотно-временной анализ и обработка сигналов: полный справочник, Elsevier Science, Оксфорд, 2003 г. ISBN  0-08-044335-4
  32. ^ Николич, Д .; Muresan, R.C .; Feng, W .; Зингер, W. (2012). «Масштабированный корреляционный анализ: лучший способ вычисления кросс-коррелограммы». Европейский журнал нейробиологии. 35 (5): 742–762. Дои:10.1111 / j.1460-9568.2011.07987.x. PMID  22324876. S2CID  4694570.
  33. ^ а б Сакоэ, Хироаки; Чиба, Сейби (1978). «Оптимизация алгоритма динамического программирования для распознавания речи». Транзакции IEEE по акустике, речи и обработке сигналов. 26. С. 43–49. Дои:10.1109 / ТАССП.1978.1163055. S2CID  17900407. Отсутствует или пусто | название = (помощь)
  34. ^ Гутте, Кирилл; Тофт, Питер; Роструп, Эгилл; Nielsen, Finn Å .; Хансен, Ларс Кай (1999). «О кластеризации временных рядов фМРТ». NeuroImage. 9. С. 298–310. Дои:10.1006 / nimg.1998.0391. PMID  10075900. S2CID  14147564. Отсутствует или пусто | название = (помощь)
  35. ^ Морманн, Флориан; Andrzejak, Ralph G .; Elger, Christian E .; Ленертц, Клаус (2007). «Предсказание захвата: долгая и извилистая дорога». Мозг. 130 (2): 314–333. Дои:10.1093 / мозг / awl241. PMID  17008335.
  36. ^ Земля, Брюс; Элиас, Дамиан. «Измерение« сложности »временного ряда».
  37. ^ [1] Чевырев И., Кормилицин А. (2016) »Учебник по методу подписи в машинном обучении, arXiv: 1603.03788v1 "
  38. ^ Ropella, G.E.P .; Nag, D.A .; Хант, К. А. (2003). «Меры сходства для автоматического сравнения результатов экспериментов in silico и in vitro». Инженерное общество медицины и биологии. 3: 2933–2936. Дои:10.1109 / IEMBS.2003.1280532. ISBN  978-0-7803-7789-9. S2CID  17798157.
  39. ^ Томинский, Кристиан; Айгнер, Вольфганг. "Браузер TimeViz: визуальный обзор методов визуализации данных, ориентированных на время". Получено 1 июня 2014.

дальнейшее чтение

  • Коробка, Джордж; Дженкинс, Гвилим (1976), Анализ временных рядов: прогнозирование и управление, ред. изд., Окленд, Калифорния: Холден-Дэй
  • Дурбин Дж., Купман С.Дж. (2001), Анализ временных рядов методами пространства состояний, Oxford University Press.
  • Гершенфельд, Нил (2000), Природа математического моделирования, Издательство Кембриджского университета, ISBN  978-0-521-57095-4, OCLC  174825352
  • Гамильтон, Джеймс (1994), Анализ временных рядов, Princeton University Press, ISBN  978-0-691-04289-3
  • Пристли, М. Б. (1981), Спектральный анализ и временные ряды, Академическая пресса. ISBN  978-0-12-564901-8
  • Шаша, Д. (2004), Открытие высокой производительности во временных рядах, Springer, ISBN  978-0-387-00857-8
  • Шамуэй Р. Х., Стоффер Д. С. (2017), Анализ временных рядов и его приложения: с примерами R (изд. 4), Спрингер, ISBN  978-3-319-52451-1
  • Вейгенд А. С., Гершенфельд Н. А. (ред.) (1994), Прогнозирование временных рядов: прогнозирование будущего и понимание прошлого. Труды Семинара перспективных исследований НАТО по сравнительному анализу временных рядов (Санта-Фе, май 1992 г.), Эддисон-Уэсли.
  • Винер, Н. (1949), Экстраполяция, интерполяция и сглаживание стационарных временных рядов, MIT Press.
  • Вудворд, У. А., Грей, Х. Л. и Эллиотт, А. С. (2012), Прикладной анализ временных рядов, CRC Press.

внешняя ссылка